《2025年全品学练考九年级数学上册苏科版江苏专版》

22. (6 分) 已知关于 $ x $ 的方程 $ x ^ { 2 } - 6 x + m ^ { 2 } - 3 m = 0 $ 的一个根为 2.
(1) 求 $ 5 m ^ { 2 } - 15 m - 100 $ 的值;
(2) 求方程的另一个根.

答案： 1. （1）
因为$x = 2$是方程$x^{2}-6x + m^{2}-3m = 0$的一个根，将$x = 2$代入方程：
得$2^{2}-6×2 + m^{2}-3m = 0$。
即$4 - 12+m^{2}-3m = 0$，化简得$m^{2}-3m=8$。
对于$5m^{2}-15m - 100$，提取公因式$5$：
$5m^{2}-15m - 100 = 5(m^{2}-3m)-100$。
把$m^{2}-3m = 8$代入上式，得$5×8-100$。
先算乘法$5×8 = 40$，再算减法$40-100=-60$。
2. （2）
设方程$x^{2}-6x + m^{2}-3m = 0$的另一个根为$x_1$。
根据韦达定理：对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，两根$x_1,x_2$有$x_1 + x_2=-\frac{b}{a}$。
在方程$x^{2}-6x + m^{2}-3m = 0$中，$a = 1$，$b=-6$，已知一个根$x = 2$，设另一个根为$x_1$，则$x_1 + 2=-\frac{-6}{1}=6$。
解得$x_1=6 - 2 = 4$。
综上，（1）$5m^{2}-15m - 100$的值为$-60$；（2）方程的另一个根为$4$。

23. (8 分) (2023 襄阳) 关于 $ x $ 的一元二次方程 $ x ^ { 2 } + 2 x + 3 - k = 0 $ 有两个不相等的实数根.
(1) 求 $ k $ 的取值范围;
(2) 若方程的两个根为 $ \alpha , \beta $,且 $ k ^ { 2 } = \alpha \beta + 3 k $,求 $ k $ 的值.

答案： $(1)$ 求$k$的取值范围
解：对于一元二次方程$ax^{2}+bx+c = 0(a\neq0)$，其判别式$\Delta=b^{2}-4ac$。
在方程$x^{2}+2x + 3 - k = 0$中，$a = 1$，$b = 2$，$c = 3 - k$。
因为方程有两个不相等的实数根，所以$\Delta＞0$。
即$\Delta = 2^{2}-4×1×(3 - k)＞0$，
展开式子得$4-12 + 4k＞0$，
移项可得$4k＞12 - 4$，
即$4k＞8$，
两边同时除以$4$，解得$k＞2$。
$(2)$ 求$k$的值
解：根据韦达定理，对于一元二次方程$ax^{2}+bx+c = 0(a\neq0)$，若方程的两根为$x_{1}$和$x_{2}$，则$x_{1}x_{2}=\frac{c}{a}$。
在方程$x^{2}+2x + 3 - k = 0$中，$\alpha\beta=\frac{3 - k}{1}=3 - k$。
已知$k^{2}=\alpha\beta+3k$，将$\alpha\beta = 3 - k$代入可得：
$k^{2}=3 - k+3k$，
整理得$k^{2}-2k - 3 = 0$，
因式分解得$(k - 3)(k + 1)=0$，
则$k - 3 = 0$或$k + 1 = 0$，
解得$k_{1}=3$，$k_{2}=-1$。
又因为由$(1)$知$k＞2$，所以$k = 3$。
综上，$(1)$$\boldsymbol{k＞2}$；$(2)$$\boldsymbol{k = 3}$。

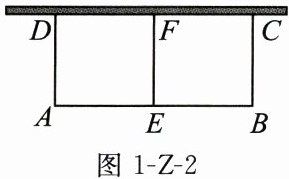
24. (8 分) 某农户为了提高经济收人,购买了 33 m 的铁栅栏,准备用这些铁栅栏靠墙(墙长 15 m)围建一个中间带有铁栅栏(垂直于墙)的矩形养鸡场(如图 1-Z-2 所示).
(1) 若要建的矩形养鸡场面积为 $ 90 \mathrm { m } ^ { 2 } $,求养鸡场的长( $ A B $ )和宽( $ B C $ );
(2) 该农户想要建一个面积为 $ 100 \mathrm { m } ^ { 2 } $ 的矩形养鸡场,这一想法能实现吗?请说明理由.

答案：
(1)养鸡场的长(AB)为15m,宽(BC)为6m
(2)不能.理由略