《2025年全品学练考九年级数学上册苏科版江苏专版》

22. (6分)如图2-Z-18,AB为$\odot O$的直径,CB是$\odot O$的切线,D为$\odot O$外一点,AD交$\odot O$于点E,$AB = AD$,$DC \perp CB$,垂足为C.
(1)求证:$DC = DE$;
(2)若$DE = 2$,$BC = 6$,求AB的长.

答案：

(1)证明:如图,连接$BD$,$BE$.
　
∵$AB$是$\odot O$的直径，
　
∴$\angle AEB = 90^{\circ}$，
　
∴$\angle BED = 90^{\circ}$.
　　　　　　　　　　　
　
∵$DC\perp BC$，
　
∴$\angle C = \angle BED = 90^{\circ}$.
　
∵$AB = AD$，
∴$\angle EDB = \angle ABD$.
　
∵$CB$是$\odot O$的切线，
∴$AB\perp BC$，
　
∴$DC// AB$，
∴$\angle CDB = \angle ABD$，
　
∴$\angle EDB = \angle CDB$.
　　又
∵$BD = BD$，
　
∴$\triangle BED\cong \triangle BCD(AAS)$，
∴$DE = DC$.
(2)10
由树状图知，共有16种等可能的结果，其中至少有1张印有“兰”字的有7种结果，
　
∴至少有1张印有“兰”字的概率为$\frac{7}{16}$.

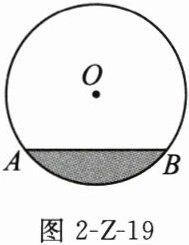
23. (8分)在底面圆半径为17dm的圆柱形油罐内装进一些油后,横截面如图2-Z-19.
(1)若油面宽$AB = 16dm$,求油的最大深度;
(2)在(1)的条件下,向油罐内再装进一些油后,若油面宽变为30dm,求油面上升了多少.

答案：
(1)$2dm$
(2)$7dm$或$23dm$

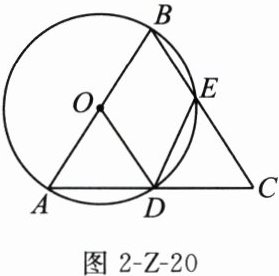
24. (8分)如图2-Z-20,在等腰三角形ABC中,$AB = BC$,以AB为直径的$\odot O$分别与AC,BC相交于点D,E,连接OD,DE.求证:
(1)$OD // BC$;
(2)$AD = DE$.

答案： 1. 证明$OD// BC$：
解：因为$AB = BC$，所以$\angle A=\angle C$。
又因为$OA = OD$（同圆半径相等），所以$\angle A=\angle ODA$。
则$\angle ODA=\angle C$（等量代换）。
根据同位角相等，两直线平行，可得$OD// BC$。
2. 证明$AD = DE$：
解：连接$BE$。
因为$AB$是$\odot O$的直径，所以$\angle AEB = 90^{\circ}$（直径所对的圆周角是直角），即$BE\perp AC$。
又因为$AB = BC$，根据等腰三角形三线合一，$BE$平分$\angle ABC$，所以$\angle ABE=\angle CBE$。
因为$\angle ADE$和$\angle ABE$所对的弧都是$\overset{\frown}{AE}$，$\angle DAE$和$\angle DBE$所对的弧都是$\overset{\frown}{DE}$。
且$\angle ABE=\angle CBE$，$\angle ADE=\angle ABE$（同弧所对的圆周角相等），$\angle DAE=\angle DBE$（同弧所对的圆周角相等）。
又因为$\angle A=\angle C$，$\angle ODA=\angle C$，$\angle A=\angle ODA$，$\angle ADE+\angle ODE=\angle ODA$，$\angle DAE+\angle C=\angle ABC$，$\angle ABE=\angle CBE$，$\angle ADE=\angle ABE$，$\angle DAE=\angle DBE$，$\angle ABE=\angle CBE$。
由$\angle ADE$和$\angle DAE$所对的弧分别为$\overset{\frown}{AE}$和$\overset{\frown}{DE}$，且$\angle ADE=\angle DAE$（等角对等弧）。
根据等角对等边，在$\triangle ADE$中，$\angle ADE=\angle DAE$，所以$AD = DE$。
综上，
(1)得证$OD// BC$；
(2)得证$AD = DE$。