《2025年全品学练考九年级数学上册苏科版江苏专版》

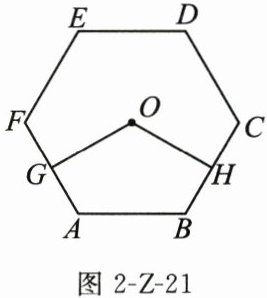
25. (8分)如图2-Z-21,已知点O是正六边形ABCDEF的对称中心,G,H分别是AF,BC上的点,且$AG = BH$.
(1)求$∠FAB$的度数;
(2)求证:$OG = OH$.

答案： 1. 求$\angle FAB$的度数：
解：正$n$边形内角和公式为$(n - 2)×180^{\circ}$（$n\geqslant3$且$n$为整数）。
对于正六边形$ABCDEF$，$n = 6$，则内角和为$(6 - 2)×180^{\circ}=720^{\circ}$。
因为正六边形的$6$个内角都相等，所以$\angle FAB=\frac{(6 - 2)×180^{\circ}}{6}=120^{\circ}$。
2. 求证$OG = OH$：
证明：连接$OA$，$OB$。
因为点$O$是正六边形$ABCDEF$的对称中心，所以$OA = OB$，$\angle OAF=\angle OBC$。
又已知$AG = BH$。
在$\triangle OAG$和$\triangle OBH$中：
$\begin{cases}OA = OB\\\angle OAG=\angle OBH\\AG = BH\end{cases}$
根据$SAS$（边角边）判定定理，可得$\triangle OAG\cong\triangle OBH$。
所以$OG = OH$（全等三角形的对应边相等）。
综上，（1）$\angle FAB = 120^{\circ}$；（2）证明过程如上述。

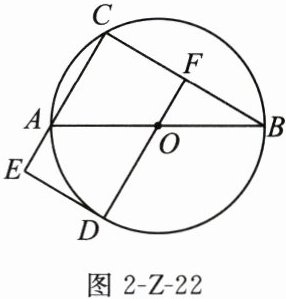
26. (12分)如图2-Z-22,AB是$\odot O$的直径,C是$\odot O$上的一点,连接BC,F为BC的中点,连接FO并延长交$\odot O$于点D,过点D的切线与CA的延长线交于点E.
(1)求证:四边形CEDF是矩形;
(2)若$AC = OA = 2$,求AE的长.

答案：
(1)证明:
∵$AB$是$\odot O$的直径，
　
∴$\angle ACB = 90^{\circ}$，
　
∴$AC\perp BC$.
　
∵$O$为$AB$的中点，$F$为$BC$的中点，
　
∴$OF// AC$，
∴$OF\perp BC$，
　
∴$\angle CFD = 90^{\circ}$.
　
∵$DE$是$\odot O$的切线，
　
∴$\angle EDF = 90^{\circ}$，
　
∴四边形$CEDF$是矩形.
(2)1

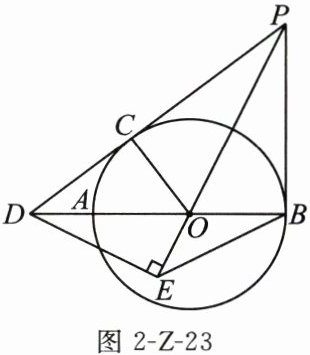
27. (12分)如图2-Z-23,AB为$\odot O$的直径,PC是$\odot O$的切线,延长PC与BA的延长线交于点D,$DE \perp PO$交PO的延长线于点E,连接OC,PB,已知$PB = 3$,$DB = 4$,$∠EDB = ∠EPB$.
(1)求证:PB是$\odot O$的切线;
(2)连接BE,求BE的长.

答案：
(1)证明:
∵$DE\perp PE$，
∴$\angle DEO = 90^{\circ}$.
　
∵$\angle EDB = \angle EPB$，$\angle DOE = \angle POB$，
　
∴$\angle OBP = \angle DEO = 90^{\circ}$，
　
∴$OB\perp PB$.
　　又
∵$OB$为$\odot O$的半径，
　
∴$PB$为$\odot O$的切线.
(2)$\sqrt{5}$