《2025年综合应用创新题典中点九年级数学上册北师大版》

1. 如图,正方形的面积为24,$△ABE$是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,要使$PD+PE$最小,则这个最小值为 ()

A. $\sqrt{3}$
B. $2\sqrt{3}$
C. $2\sqrt{6}$
D. $\sqrt{6}$

答案：
C [点拨]如图,设BE与AC交于点P',连接PB.
　　　　　　　　
∵四边形ABCD为正方形，
∴点B与点D关于AC对称,
∴PD=PB.
∴PD+PE=PB+PE.
由两点之间线段最短可知，当点P在P'处时，PB+PE的值最小,即PD+PE的值最小,最小值等于BE的长.
∵正方形ABCD的面积为24,
∴AB=2√6.
又
∵△ABE是等边三角形，
∴BE=AB=2√6.
故选C.

2. [2023广州] 如图,正方形ABCD的边长为4,点E在边BC上,且$BE= 1$,F为对角线BD上一动点,连接CF,EF,则$CF+EF$的最小值为______.

答案： $\sqrt{17}$

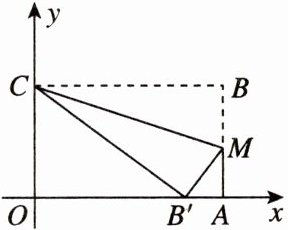
3. 如图,长方形OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴上,点C在y轴上,$OA= 10$,$OC= 6$,在AB上取一点M,使得$△CBM$沿CM翻折后,点B落在x轴上,记作点$B'$.
(1)求点$B'$的坐标;
(2)求折痕CM所在直线的表达式.
(3)折痕CM上是否存在一点P,使$PO+PB'$的值最小? 若存在,请求出最小值,若不存在,请说明理由.

答案：
[解]
(1)
∵四边形OABC是长方形,OA=10，
∴BC=OA=10,∠AOC=90°.
由折叠的性质得B'C=BC=10.
在Rt△B'OC中,B'C=10,OC=6,
∴B'O=√(B'C² - OC²)=8.
∴点B'的坐标为(8,0).
(2)由长方形的性质可得AB=OC=6,∠BAO=90°.
设AM=x,则BM=AB - AM=6 - x.
∵OA=10,B'O=8,
∴B'A=2.
由折叠的性质得B'M=BM=6 - x.
在Rt△AB'M中,B'A² + AM² = B'M²,
∴2² + x² = (6 - x)²,解得x=$\frac{8}{3}$.
∴M(10,$\frac{8}{3}$).
∵OC=6,
∴C(0,6).
设折痕CM所在直线的表达式为y=kx+b.
将C(0,6),M(10,$\frac{8}{3}$)的坐标代入，得$\begin{cases}6 = b,\\\frac{8}{3} = 10k + b,\end{cases}$
解得$\begin{cases}k = -\frac{1}{3},\\b = 6.\end{cases}$
∴折痕CM所在直线的表达式为y = -$\frac{1}{3}$x + 6.
(3)折痕CM上存在一点P，使PO + PB'的值最小.连接OB，OB与CM的交点即为所求点P，如图.
　　　　　　　　
∵△CBM沿CM翻折后，点B落在点B'处，
∴PB = PB'.
∴PO + PB' = PO + PB = OB.
∵OB = √(OA² + AB²)=√(10² + 6²)=2√34,
∴PO + PB'的最小值为2√34.