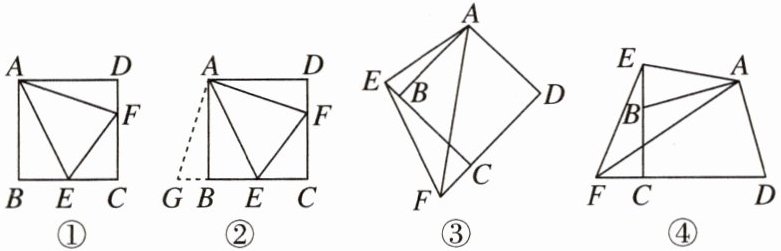
4. 如图①, 四边形 ABCD 是正方形, E, F 分别在边 BC, CD 上, 且 $ \angle EAF = 45^\circ $, 我们把这种模型称为“半角模型”, 在解决“半角模型”问题时, 旋转是一种常用的方法.
(1) 在图②中, 为了证明结论“ $ EF = BE + DF $ ”, 小亮将 $ \triangle ADF $ 绕点 A 顺时针旋转 $ 90^\circ $ 后解决了这个问题, 请按小亮的思路写出证明过程;
(2) 如图③, 当 $ \angle EAF $ 绕点 A 旋转到图③位置时, 试探究 EF 与 DF, BE 之间有怎样的数量关系;
(3) 如图④, 如果四边形 ABCD 中, $ AB = AD $, $ \angle BAD = \angle BCD = 90^\circ $, $ \angle EAF = 45^\circ $, 且 $ BC = 7 $, $ DC = 13 $, $ CF = 5 $, 求 BE 的长.
(1) 在图②中, 为了证明结论“ $ EF = BE + DF $ ”, 小亮将 $ \triangle ADF $ 绕点 A 顺时针旋转 $ 90^\circ $ 后解决了这个问题, 请按小亮的思路写出证明过程;
(2) 如图③, 当 $ \angle EAF $ 绕点 A 旋转到图③位置时, 试探究 EF 与 DF, BE 之间有怎样的数量关系;
(3) 如图④, 如果四边形 ABCD 中, $ AB = AD $, $ \angle BAD = \angle BCD = 90^\circ $, $ \angle EAF = 45^\circ $, 且 $ BC = 7 $, $ DC = 13 $, $ CF = 5 $, 求 BE 的长.

答案:
(1)[证明]
∵四边形ABCD为正方形,
∴∠ABC=∠D=∠BAD=90°.
由旋转可得GB=DF,AF=AG,∠BAG=∠DAF,∠D=∠ABG=90°,
∴∠ABC+∠ABG=180°.
∴点G,B,C三点共线.
∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠EAF.
在△AGE和△AFE中,{AG=AF,∠GAE=∠FAE,AE=AE,
∴△AGE≌△AFE(SAS).
∴GE=EF.
∵GE=GB+BE=DF+BE,
∴EF=BE+DF.
(2)[解]如图①,把△ABE绕点A逆时针旋转90°得到△ADG,则DG=BE;

同
(1)可证得△AEF≌△AGF(SAS),
∴EF=GF.
∴EF=DF−DG=DF−BE.
(3)[解]如图②,在DC上取一点G,使得DG=BE,连接AG.

∵∠BAD=∠BCD=90°,
∴∠ABC+∠D=180°.
又
∵∠ABE+∠ABC=180°,
∴∠ABE=∠D,
又
∵AB=AD,BE=DG,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=45°,
∴∠EAB+∠BAF=∠DAG+∠BAF=45°.
∵∠BAD=90°,
∴∠FAG=∠FAE=45°.
又
∵AE=AG,AF=AF,
∴△AFE≌△AFG(SAS).
∴EF=FG.
设BE=x,则EC=EB+BC=x+7,EF=FG=18−x.在Rt△ECF中,
∵EF²=EC²+CF²,
∴(18−x)²=(7+x)²+5².
∴x=5,即BE=5.
(1)[证明]
∵四边形ABCD为正方形,
∴∠ABC=∠D=∠BAD=90°.
由旋转可得GB=DF,AF=AG,∠BAG=∠DAF,∠D=∠ABG=90°,
∴∠ABC+∠ABG=180°.
∴点G,B,C三点共线.
∵∠EAF=45°,
∴∠BAE+∠DAF=45°.
∴∠BAG+∠BAE=45°.
∴∠GAE=∠EAF.
在△AGE和△AFE中,{AG=AF,∠GAE=∠FAE,AE=AE,
∴△AGE≌△AFE(SAS).
∴GE=EF.
∵GE=GB+BE=DF+BE,
∴EF=BE+DF.
(2)[解]如图①,把△ABE绕点A逆时针旋转90°得到△ADG,则DG=BE;

同
(1)可证得△AEF≌△AGF(SAS),
∴EF=GF.
∴EF=DF−DG=DF−BE.
(3)[解]如图②,在DC上取一点G,使得DG=BE,连接AG.

∵∠BAD=∠BCD=90°,
∴∠ABC+∠D=180°.
又
∵∠ABE+∠ABC=180°,
∴∠ABE=∠D,
又
∵AB=AD,BE=DG,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=45°,
∴∠EAB+∠BAF=∠DAG+∠BAF=45°.
∵∠BAD=90°,
∴∠FAG=∠FAE=45°.
又
∵AE=AG,AF=AF,
∴△AFE≌△AFG(SAS).
∴EF=FG.
设BE=x,则EC=EB+BC=x+7,EF=FG=18−x.在Rt△ECF中,
∵EF²=EC²+CF²,
∴(18−x)²=(7+x)²+5².
∴x=5,即BE=5.
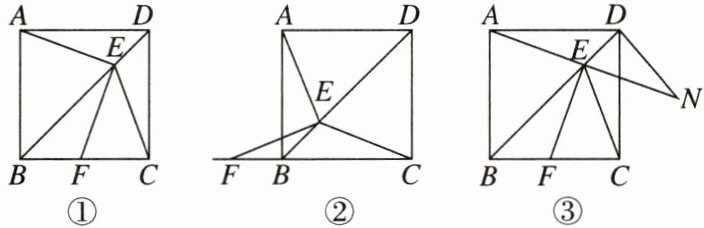
5. (新视角 综合探究题) 如图, 在正方形 ABCD 中, 点 E 是对角线 BD 上一点, 连接 EA, 将线段 EA 绕点 E 逆时针旋转, 使点 A 落在射线 CB 上的点 F 处, 连接 EC.
问题引入: (1) 请你在图①或图②中证明 $ EF = EC $ (选择一种情况即可);
探索发现: (2) 在 (1) 中你选择的图形上继续探索: 延长 FE 交直线 CD 于点 M. 将图形补充完整, 猜想线段 DM 和线段 BF 的数量关系, 并说明理由;
拓展应用: (3) 如图③, $ AB = 3 $, 延长 AE 至点 N, 使 $ NE = AE $, 连接 DN. 当 $ \triangle ADN $ 的周长最小时, 请你直接写出 $ \triangle ADN $ 的周长.
问题引入: (1) 请你在图①或图②中证明 $ EF = EC $ (选择一种情况即可);
探索发现: (2) 在 (1) 中你选择的图形上继续探索: 延长 FE 交直线 CD 于点 M. 将图形补充完整, 猜想线段 DM 和线段 BF 的数量关系, 并说明理由;
拓展应用: (3) 如图③, $ AB = 3 $, 延长 AE 至点 N, 使 $ NE = AE $, 连接 DN. 当 $ \triangle ADN $ 的周长最小时, 请你直接写出 $ \triangle ADN $ 的周长.

答案:
(1)[证明]选择题图①:
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°.
又
∵BE=BE,
∴△BEA≌△BEC(SAS).
∴EA=EC.
由旋转得EA=EF,
∴EF=EC.
选择题图②:
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°.
又
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC.
由旋转得EA=EF,
∴EF=EC.
(2)[解]猜想DM=BF.理由如下:
选择题图①:如图①,过点F作FH⊥BC交BD于点H,则∠HFB=90°.

∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠HFB=∠BCD.
∴FH//CD.
∴∠HFE=∠M.
∵EF=EC,
∴∠EFC=∠ECF.
∵∠FCD=90°,
∴∠EFC+∠M=90°,∠ECD+∠ECF=90°.
∴∠M=∠ECM.
∴EC=EM.
∴EF=EM.
又
∵∠HEF=∠DEM,∠HFE=∠M,
∴△HEF≌△DEM(ASA).
∴DM=FH.
∵∠HBF=45°,∠BFH=90°,
∴∠BHF=45°=∠HBF.
∴BF=FH,
∴DM=BF.
选择题图②:如图②,过点F作FH⊥BC交DB的延长线于点H,则∠HFB=90°.

∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠HFB=∠BCD.
∴FH//CD.
∴∠H=∠EDM.
∵EF=EC,
∴∠EFC=∠ECF.
∵∠EFC+∠FMC=90°,∠ECF+∠ECM=90°,
∴∠FMC=∠ECM.
∴EC=EM.
∴EF=EM;
又
∵∠HEF=∠DEM,∠H=∠EDM,
∴△HEF≌△DEM(AAS),
∴FH=DM.
∵∠FBH=∠DBC=45°,
∴∠H=45°.
∴BF=FH.
∴DM=BF.
(3)[解]△ADN的周长最小为3+ 3√5.[点拨]如图③,
取AD的中点G,连接EG,则DG=$\frac{1}{2}$AD.


在正方形ABCD中,AD=CD=AB=3,∠ADC=90°.
∵NE=AE,
∴点E是AN的中点.
∴EG=$\frac{1}{2}$DN.
由
(1)可得EA=EC.
∴△ADN的周长=AD+AN+DN=3+2(AE+EG)=3+2(CE+EG),
∴当△ADN的周长最小时,CE+EG的值最小,此时C,
E,G三点共线,如图④.
∵GC= $\sqrt{(\frac{3}{2})²+3²}$=$\frac{3\sqrt{5}}{2}$,
∴△ADN的周长最小为3+ 3√5
(1)[证明]选择题图①:
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°.
又
∵BE=BE,
∴△BEA≌△BEC(SAS).
∴EA=EC.
由旋转得EA=EF,
∴EF=EC.
选择题图②:
∵四边形ABCD是正方形,
∴BA=BC,∠ABE=∠CBE=45°.
又
∵BE=BE,
∴△BEA≌△BEC(SAS),
∴EA=EC.
由旋转得EA=EF,
∴EF=EC.
(2)[解]猜想DM=BF.理由如下:
选择题图①:如图①,过点F作FH⊥BC交BD于点H,则∠HFB=90°.

∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠HFB=∠BCD.
∴FH//CD.
∴∠HFE=∠M.
∵EF=EC,
∴∠EFC=∠ECF.
∵∠FCD=90°,
∴∠EFC+∠M=90°,∠ECD+∠ECF=90°.
∴∠M=∠ECM.
∴EC=EM.
∴EF=EM.
又
∵∠HEF=∠DEM,∠HFE=∠M,
∴△HEF≌△DEM(ASA).
∴DM=FH.
∵∠HBF=45°,∠BFH=90°,
∴∠BHF=45°=∠HBF.
∴BF=FH,
∴DM=BF.
选择题图②:如图②,过点F作FH⊥BC交DB的延长线于点H,则∠HFB=90°.

∵四边形ABCD是正方形,
∴∠BCD=90°.
∴∠HFB=∠BCD.
∴FH//CD.
∴∠H=∠EDM.
∵EF=EC,
∴∠EFC=∠ECF.
∵∠EFC+∠FMC=90°,∠ECF+∠ECM=90°,
∴∠FMC=∠ECM.
∴EC=EM.
∴EF=EM;
又
∵∠HEF=∠DEM,∠H=∠EDM,
∴△HEF≌△DEM(AAS),
∴FH=DM.
∵∠FBH=∠DBC=45°,
∴∠H=45°.
∴BF=FH.
∴DM=BF.
(3)[解]△ADN的周长最小为3+ 3√5.[点拨]如图③,
取AD的中点G,连接EG,则DG=$\frac{1}{2}$AD.


在正方形ABCD中,AD=CD=AB=3,∠ADC=90°.
∵NE=AE,
∴点E是AN的中点.
∴EG=$\frac{1}{2}$DN.
由
(1)可得EA=EC.
∴△ADN的周长=AD+AN+DN=3+2(AE+EG)=3+2(CE+EG),
∴当△ADN的周长最小时,CE+EG的值最小,此时C,
E,G三点共线,如图④.
∵GC= $\sqrt{(\frac{3}{2})²+3²}$=$\frac{3\sqrt{5}}{2}$,
∴△ADN的周长最小为3+ 3√5
查看更多完整答案,请扫码查看


