《2025年综合应用创新题典中点九年级数学上册北师大版》

2. (新视角 探究题) 问题情境: 如图①, 在正方形 ABCD 中, E 为边 BC 上一点 (不与点 B, C 重合), 垂直于 AE 的一条直线 MN 分别交 AB, AE, CD 于点 M, P, N. 判断线段 DN, MB, EC 之间的数量关系, 并说明理由;
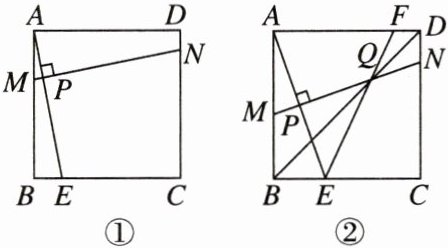
问题探究: 在“问题情境”的基础上, 如图②, 若垂足 P 恰好为 AE 的中点, 连接 BD, 交 MN 于点 Q, 连接 EQ 并延长, 交边 AD 于点 F, 求 $ \angle AEF $ 的度数.

答案：
[解]问题情境:
　线段DN,MB,EC之间的数量关系为DN+MB=EC.理由如下:
∵四边形ABCD是正方形，
∴∠ABE=∠BCD=90°,AB=BC=CD,AB//CD.
　过点B作BF//MN,分别交AE,CD于点G,F,如图①所示
∴四边形MBFN为平行四边形,
∴NF=MB.
∵AE⊥MN,MN//BF,
　　　　　　　　　　　　　　　　　　　　　
∴BF⊥AE.
∴∠BGE=90°.
∴∠CBF+∠AEB=90°.
　又
∵∠BAE+∠AEB=90°,
∴∠CBF=∠BAE;
　在△ABE和△BCF中,{∠BAE=∠CBF,AB=BC,∠ABE=∠BCF=90°,
∴△ABE≌△BCF(ASA).
∴BE=CF.
∵CD=BC,即DN+NF+CF=BE+EC,
∴DN+MB=EC.
　问题探究:
　连接AQ,过点Q作HI//AB,分别交AD,BC于点H,I,如图②所示
∵四边形ABCD是正方形,
∴AB=AD,易得四边形ABIH为矩形.
∴HI⊥AD,HI⊥BC,HI=AB=AD.
∵BD是正方形ABCD的对角线，
∴∠BDA=45°.
∴△DHQ是等腰直角三角形.
∴HD=HQ.
　　　　　　　　　　　　　　　　　　　　　
∴AD−HD=HI−HQ,即AH=QI.
∵MN是AE的垂直平分线，
∴AQ=QE.
　在Rt△AHQ和Rt△QIE中,{AQ=QE,AH=QI,
∴Rt△AHQ≌△Rt△QIE(HL).
∴∠AQH=∠QEI.
∴∠AQH+∠EQI=90°.
∴∠AQE=90°.
∴△AQE是等腰直角三角形
∴∠AEQ=45°,即∠AEF=45°.

3. (新视角 新定义题) 如图①, 四边形 ABCD 是正方形, E, F 分别在边 BC 和 CD 上, 且 $ \angle EAF = 45^\circ $, 我们把这种模型称为“半角模型”, 在解决“半角模型”问题时, 旋转是一种常用的方法. 小明为了了解线段 EF, BE, DF 之间的关系, 将 $ \triangle ADF $ 绕点 A 顺时针旋转 $ 90^\circ $ 后 (如图②) 解决了这个问题.
(1) 请直接写出线段 EF, BE, DF 之间的关系;
(2) 如图③, 在等腰直角三角形 ABD 中, $ \angle BAD = 90^\circ $, $ AB = AD $, 点 E, F 在边 BD 上, 且 $ \angle EAF = 45^\circ $, 请写出 EF, BE, DF 之间的关系, 并说明理由.

答案：
[解]
(1)EF=BE+DF.[点拨]
∵四边形ABCD为正方形，
∴∠ABC=∠D=∠BAD=90°.
　由旋转可得GB=DF,AF=AG,∠BAG=∠DAF,∠D=∠ABG=90°,
∴∠ABC+∠ABG=180°.
∴点G,B,C三点共线.
　
∵∠EAF=45°,
　
∴∠BAE+∠DAF=45°.
　
∴∠BAG+∠BAE=45°.
　
∴∠GAE=∠EAF.
　　在△AGE和△AFE中，{AG=AF,∠GAE=∠FAE,AE=AE,
　
∴△AGE≌△AFE(SAS).
　
∴GE=EF.
　
∵GE=GB+BE=DF+BE,
　
∴EF=BE+DF.
(2)EF²=BE²+DF²,理由如下:
　　把△AFD绕点A顺时针旋转90°得到△AE'B,连接EE',如图所示.
　　　　　　　　　　
　
∴BE'=FD,AE’=AF,∠D=∠ABE',∠FAD=∠E'AB.
　
∵AB=AD,
　
∴∠ABD=∠ADB=45°.
　
∴∠ABD+∠ABE'=90°,即∠E'BD=90°.
　
∴E'B²+BE²=E’E².
　
∵∠FAE=45°,∠BAD=90°,
　
∴∠BAE+∠FAD=45°,
　
∴∠E'AB+∠BAE=45°,即∠E'AE=45°.
　　在△AEE'和△AEF中,{AE=AE,∠E'AE=∠FAE,AE'=AF,
　
∴△AEE'≌△AEF(SAS).
　
∴EE'=FE.
　
∴EF²=BE²+DF².