《2025年综合应用创新题典中点九年级数学上册北师大版》

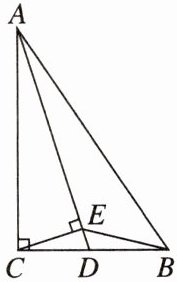
8. 如图,在 $ Rt \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,点 D 在 BC 上,连接 AD,$ CE \perp AD $,垂足为 E,连接 BE。
(1) 求证：$ \triangle CDE \backsim \triangle ADC $；
(2) 若点 D 是 BC 的中点,$ \angle BED $ 与 $ \angle ABC $ 是否相等,并说明理由。

答案：

(1)[证明]
∵CE⊥AD,
∴∠CED=90°,∠CAD+∠ECA=90°.
∵∠ACB=90°,
∴∠ECD+∠ECA=90°.
∴∠ECD=∠CAD.
　又
∵∠DEC=∠ACD=90°,
∴△CDE∽△ADC.
(2)[解]∠BED=∠ABC,理由如下:
　　由
(1)得△CDE∽△ADC,
　
∴CE:AC=ED:CD①.
　　如图，过点B作BF⊥AD,交AD的延长线于点F.
　
∵D是BC的中点,
∴CD=BD.
　
∵BF⊥AD,
　
∴∠BFD=90°=∠CED.
　　
　　又
∵∠CDE=∠BDF,
　
∴△CDE≌△BDF(AAS).
　
∴ED=FD,CE=BF②.
　　由①②可得BF:AC=CE:AC=ED:CD=2ED:2CD=EF:CB.
　
∵∠ACB=∠BFE=90°,BF:AC=EF:CB,
　
∴△ACB∽△BFE.
　
∴∠BED=∠ABC.

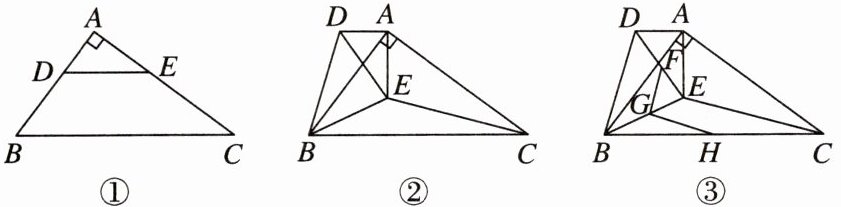
9. [2023 郴州模拟节选] 如图①,在 $ Rt \triangle ABC $ 中,$ \angle A = 90^{\circ} $,$ AB = 9 $,$ AC = 12 $,点 D 是 AB 上一点(不与点 A,B 重合),作 $ DE // BC $,交 AC 于点 E。如图②,把 $ \triangle ADE $ 绕点 A 顺时针旋转 $ \alpha $ 度 $ (0 ＜ \alpha ＜ 90) $,连接 BD,BE,CE。在 $ \triangle ADE $ 旋转的过程中,完成以下问题：
(1) 如图②,求证：$ \triangle ADB \backsim \triangle AEC $；
(2) 如图③,若点 F,H,G 分别是 DE,BC,BE 的中点,求 $ \frac{GF}{GH} $ 的值。

答案：
(1)[证明]
∵△ADE绕点A旋转前,DE//BC,
∴易得△ADE∽△ABC;
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$,即$\frac{AD}{AE}$=$\frac{AB}{AC}$.
　由旋转得∠DAE=∠BAC,
∴∠DAB+∠BAE=∠CAE+∠BAE.
∴∠DAB=∠CAE.
　又
∵$\frac{AD}{AE}$=$\frac{AB}{AC}$,
∴△ADB∽△AEC.
(2)[解]
∵点F,H,G分别是DE,BC,BE的中点，
　
∴GH是△BCE的中位线,GF是△BED的中位线.
　
∴GH=$\frac{1}{2}$EC,GF=$\frac{1}{2}$BD.
　　由
(1)得△ADB∽△AEC,且AB=9,AC=12.
　
∴$\frac{DB}{EC}$=$\frac{AB}{AC}$=$\frac{3}{4}$.
　
∴$\frac{GF}{GH}$=$\frac{\frac{1}{2}DB}{\frac{1}{2}EC}$=$\frac{DB}{EC}$=$\frac{3}{4}$.