5. 情境题 主题教学 在综合与实践课上,老师组织同学们以“矩形的折叠”为主题开展数学活动。
问题情景:在矩形$ABCD$中,点$E为AD$边上一动点,点$F为BC$边上一点,连接$EF$,将四边形$CDEF沿EF$折叠,点$C$,$D分别落在点C'$,$D'$处,设$\angle EFC = \alpha$。
(1) 如图①,若$\angle EFC = 75^{\circ}$,$AD = AB$,点$F为BC$的中点,延长$D'C'交AB于点P$,则$PC'与PB$的数量关系是______,写出图中一个$30^{\circ}$的角:______;
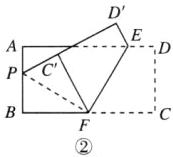
(2) 如图②,若点$F为BC$的中点,$AD = 2AB$,$45^{\circ} < \alpha < 90^{\circ}$,延长$D'C'交AB于点P$。求$PC'与PB$的数量关系,并说明理由;
(3) 如图③,若$AB = 3$,$AD = 6$,$BF = 1$,连接$C'E$,当点$E为AD$的三等分点时,直接写出$\frac{E F}{C'E}$的值。
F}{C'E}$的值。
问题情景:在矩形$ABCD$中,点$E为AD$边上一动点,点$F为BC$边上一点,连接$EF$,将四边形$CDEF沿EF$折叠,点$C$,$D分别落在点C'$,$D'$处,设$\angle EFC = \alpha$。
(1) 如图①,若$\angle EFC = 75^{\circ}$,$AD = AB$,点$F为BC$的中点,延长$D'C'交AB于点P$,则$PC'与PB$的数量关系是______,写出图中一个$30^{\circ}$的角:______;
(2) 如图②,若点$F为BC$的中点,$AD = 2AB$,$45^{\circ} < \alpha < 90^{\circ}$,延长$D'C'交AB于点P$。求$PC'与PB$的数量关系,并说明理由;
(3) 如图③,若$AB = 3$,$AD = 6$,$BF = 1$,连接$C'E$,当点$E为AD$的三等分点时,直接写出$\frac{E
 F}{C'E}$的值。
F}{C'E}$的值。
答案:
【解】
(1)$PC'=PB$;$∠BFC'$(答案不唯一)
【点拨】如图①,连接$PF$.
∵$F$为$BC$的中点,
∴$BF=CF$.
∵四边形$ABCD$为矩形,
∴$∠B=∠C=90^{\circ}$.
∵将四边形$CDEF$沿$EF$折叠,点$C$,$D$分别落在点$C'$,$D'$处,
∴$FC=FC'$,$∠C=∠D'C'F=90^{\circ}$.
∴$∠PC'F=90^{\circ}$,$BF=C'F$.
又
∵$PF=PF$,
∴$Rt\triangle PBF\cong Rt\triangle PC'F(HL)$.
∴$PB=PC'$.
由折叠性质得$∠EFC'=∠EFC=75^{\circ}$.
∴$∠BFC'=180^{\circ}-∠EFC-∠EFC'=30^{\circ}$.

(2)$PC'=PB$.理由如下:
如图②,连接$PF$.
∵$F$为$BC$的中点,
∴$BF=CF$.
易得$∠B=∠C=90^{\circ}$.
∵将四边形$CDEF$沿$EF$折叠,点$C$,$D$分别落在点$C'$,$D'$处,
∴$FC=FC'$,$∠C=∠D'C'F=90^{\circ}$.
∴$∠PC'F=90^{\circ}$,$BF=C'F$.
又
∵$PF=PF$,
∴$Rt\triangle PBF\cong Rt\triangle PC'F(HL)$.
∴$PC'=PB$.
(3)$\frac {EF}{C'E}$的值为$\frac {\sqrt {10}}{5}$或$\frac {3\sqrt {26}}{13}$.
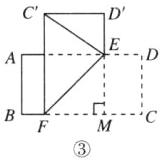
【点拨】①若点$E$为$AD$的三等分点,且$AE=2DE$.
∵$AD=6$,$AE=2DE$,
∴$AE=4$,$ED=2$.
如图③,过点$E$作$EM⊥BC$于点$M$,
易得四边形$ABME$为矩形.
∴$BM=AE=4$,$EM=AB=3$.
∴$FM=BM-BF=4-1=3$.
∴$EF=\sqrt {FM^{2}+EM^{2}}=3\sqrt {2}$.
易得$∠D=90^{\circ}$,$CD=AB$.
由折叠的性质得$ED'=ED=2$,$C'D'=CD=AB=3$,
$∠D'=∠D=90^{\circ}$.
∴$C'E=\sqrt {C'D'^{2}+D'E^{2}}=\sqrt {13}$.
∴$\frac {EF}{C'E}=\frac {3\sqrt {2}}{\sqrt {13}}=\frac {3\sqrt {26}}{13}$.
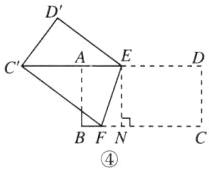
②若点$E$为$AD$的三等分点,且$DE=2AE$,易得$AE=2$,$ED=4$.
如图④,过点$E$作$EN⊥BC$于点$N$.
同理可得$FN=1$,$EN=3$,
∴$EF=\sqrt {FN^{2}+EN^{2}}=\sqrt {10}$.
同理由折叠可得$ED'=ED=4$,$C'D'=CD=AB=3$,
$∠D'=∠D=90^{\circ}$,
∴$C'E=\sqrt {C'D'^{2}+D'E^{2}}=5$.
∴$\frac {EF}{C'E}=\frac {\sqrt {10}}{5}$.
综上所述,$\frac {EF}{C'E}$的值为$\frac {\sqrt {10}}{5}$或$\frac {3\sqrt {26}}{13}$.
【解】
(1)$PC'=PB$;$∠BFC'$(答案不唯一)
【点拨】如图①,连接$PF$.
∵$F$为$BC$的中点,
∴$BF=CF$.
∵四边形$ABCD$为矩形,
∴$∠B=∠C=90^{\circ}$.
∵将四边形$CDEF$沿$EF$折叠,点$C$,$D$分别落在点$C'$,$D'$处,
∴$FC=FC'$,$∠C=∠D'C'F=90^{\circ}$.
∴$∠PC'F=90^{\circ}$,$BF=C'F$.
又
∵$PF=PF$,
∴$Rt\triangle PBF\cong Rt\triangle PC'F(HL)$.
∴$PB=PC'$.
由折叠性质得$∠EFC'=∠EFC=75^{\circ}$.
∴$∠BFC'=180^{\circ}-∠EFC-∠EFC'=30^{\circ}$.

(2)$PC'=PB$.理由如下:
如图②,连接$PF$.
∵$F$为$BC$的中点,
∴$BF=CF$.
易得$∠B=∠C=90^{\circ}$.
∵将四边形$CDEF$沿$EF$折叠,点$C$,$D$分别落在点$C'$,$D'$处,
∴$FC=FC'$,$∠C=∠D'C'F=90^{\circ}$.
∴$∠PC'F=90^{\circ}$,$BF=C'F$.
又
∵$PF=PF$,
∴$Rt\triangle PBF\cong Rt\triangle PC'F(HL)$.
∴$PC'=PB$.

(3)$\frac {EF}{C'E}$的值为$\frac {\sqrt {10}}{5}$或$\frac {3\sqrt {26}}{13}$.
【点拨】①若点$E$为$AD$的三等分点,且$AE=2DE$.
∵$AD=6$,$AE=2DE$,
∴$AE=4$,$ED=2$.
如图③,过点$E$作$EM⊥BC$于点$M$,
易得四边形$ABME$为矩形.
∴$BM=AE=4$,$EM=AB=3$.
∴$FM=BM-BF=4-1=3$.
∴$EF=\sqrt {FM^{2}+EM^{2}}=3\sqrt {2}$.
易得$∠D=90^{\circ}$,$CD=AB$.
由折叠的性质得$ED'=ED=2$,$C'D'=CD=AB=3$,
$∠D'=∠D=90^{\circ}$.
∴$C'E=\sqrt {C'D'^{2}+D'E^{2}}=\sqrt {13}$.
∴$\frac {EF}{C'E}=\frac {3\sqrt {2}}{\sqrt {13}}=\frac {3\sqrt {26}}{13}$.

②若点$E$为$AD$的三等分点,且$DE=2AE$,易得$AE=2$,$ED=4$.
如图④,过点$E$作$EN⊥BC$于点$N$.
同理可得$FN=1$,$EN=3$,
∴$EF=\sqrt {FN^{2}+EN^{2}}=\sqrt {10}$.
同理由折叠可得$ED'=ED=4$,$C'D'=CD=AB=3$,
$∠D'=∠D=90^{\circ}$,
∴$C'E=\sqrt {C'D'^{2}+D'E^{2}}=5$.
∴$\frac {EF}{C'E}=\frac {\sqrt {10}}{5}$.

综上所述,$\frac {EF}{C'E}$的值为$\frac {\sqrt {10}}{5}$或$\frac {3\sqrt {26}}{13}$.
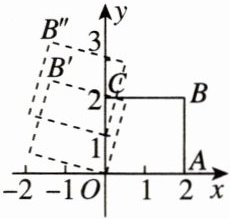
6. 如图,在直角坐标系中,边长为2个单位长度的正方形$ABCO绕原点O逆时针旋转75^{\circ}$,再沿$y$轴方向向上平移1个单位长度,则点$B''$的坐标为()
A. $(-\sqrt{2},\sqrt{6})$
B. $(-\sqrt{2},\sqrt{6} + 1)$
C. $(\sqrt{2},-\sqrt{6})$
D. $(-\sqrt{2},\sqrt{6} - 1)$

A. $(-\sqrt{2},\sqrt{6})$
B. $(-\sqrt{2},\sqrt{6} + 1)$
C. $(\sqrt{2},-\sqrt{6})$
D. $(-\sqrt{2},\sqrt{6} - 1)$
答案:
B 【点拨】过$B'$作$B'D⊥y$轴于$D$,连接$OB$,$OB'$.
∵边长为$2$个单位长度的正方形$ABCO$绕原点$O$逆时针旋转$75^{\circ}$,
∴$∠BOB'=75^{\circ}$,$∠BOC=45^{\circ}$,$OB=OB'=2\sqrt {2}$.
∴$∠B'OD=30^{\circ}$.
∴$B'D=\frac {1}{2}OB'=\sqrt {2}$.
∴$OD=\sqrt {OB'^{2}-B'D^{2}}=\sqrt {6}$.
∴$B'(-\sqrt {2},\sqrt {6})$.
∵点$B''$由点$B'$沿$y$轴方向向上平移$1$个单位长度得到,
∴$B''(-\sqrt {2},\sqrt {6}+1)$.
故选B.
∵边长为$2$个单位长度的正方形$ABCO$绕原点$O$逆时针旋转$75^{\circ}$,
∴$∠BOB'=75^{\circ}$,$∠BOC=45^{\circ}$,$OB=OB'=2\sqrt {2}$.
∴$∠B'OD=30^{\circ}$.
∴$B'D=\frac {1}{2}OB'=\sqrt {2}$.
∴$OD=\sqrt {OB'^{2}-B'D^{2}}=\sqrt {6}$.
∴$B'(-\sqrt {2},\sqrt {6})$.
∵点$B''$由点$B'$沿$y$轴方向向上平移$1$个单位长度得到,
∴$B''(-\sqrt {2},\sqrt {6}+1)$.
故选B.
7. 如图,在正方形$ABCD$中,$E$,$F是对角线BD$上两点,且$\angle EAF = 45^{\circ}$,将$\triangle ADF绕点A顺时针旋转90^{\circ}$后,得到$\triangle ABQ$,连接$EQ$。
(1) 求证:$EA是\angle QED$的平分线;
(2) 已知$BE = 1$,$DF = 2$,求$EF$的长。

(1) 求证:$EA是\angle QED$的平分线;
(2) 已知$BE = 1$,$DF = 2$,求$EF$的长。

答案:
(1)【证明】在正方形$ABCD$中,$∠BAD=90^{\circ}$.
∵将$\triangle ADF$绕点$A$顺时针旋转$90^{\circ}$后,得到$\triangle ABQ$,
∴$AQ=AF$,$∠BAQ=∠DAF$.
∵$∠EAF=45^{\circ}$,
∴$∠DAF+∠BAE=45^{\circ}$.
∴$∠QAE=45^{\circ}$.
∴$∠QAE=∠FAE$.
在$\triangle AQE$和$\triangle AFE$中,$\left\{\begin{array}{l} AQ=AF,\\ ∠QAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴$\triangle AQE\cong \triangle AFE(SAS)$.
∴$∠AEQ=∠AEF$.
∴$EA$是$∠QED$的平分线.
(2)【解】由
(1)得$\triangle AQE\cong \triangle AFE$,
∴$QE=EF$.
由题意得$QB=DF$,$∠ADF=∠ABQ$.
∵四边形$ABCD$是正方形,$BD$是对角线,
∴$∠ADB=∠ABD=45^{\circ}$.
∴$∠ABQ=45^{\circ}$.
∴$∠QBE=∠ABQ+∠ABD=90^{\circ}$.
在$Rt\triangle QBE$中,$QB^{2}+BE^{2}=QE^{2}$.
又
∵$QB=DF$,$QE=EF$,
∴$EF^{2}=BE^{2}+DF^{2}=1+4=5$.
∴$EF=\sqrt {5}$(负值已舍去).
(1)【证明】在正方形$ABCD$中,$∠BAD=90^{\circ}$.
∵将$\triangle ADF$绕点$A$顺时针旋转$90^{\circ}$后,得到$\triangle ABQ$,
∴$AQ=AF$,$∠BAQ=∠DAF$.
∵$∠EAF=45^{\circ}$,
∴$∠DAF+∠BAE=45^{\circ}$.
∴$∠QAE=45^{\circ}$.
∴$∠QAE=∠FAE$.
在$\triangle AQE$和$\triangle AFE$中,$\left\{\begin{array}{l} AQ=AF,\\ ∠QAE=∠FAE,\\ AE=AE,\end{array}\right.$
∴$\triangle AQE\cong \triangle AFE(SAS)$.
∴$∠AEQ=∠AEF$.
∴$EA$是$∠QED$的平分线.
(2)【解】由
(1)得$\triangle AQE\cong \triangle AFE$,
∴$QE=EF$.
由题意得$QB=DF$,$∠ADF=∠ABQ$.
∵四边形$ABCD$是正方形,$BD$是对角线,
∴$∠ADB=∠ABD=45^{\circ}$.
∴$∠ABQ=45^{\circ}$.
∴$∠QBE=∠ABQ+∠ABD=90^{\circ}$.
在$Rt\triangle QBE$中,$QB^{2}+BE^{2}=QE^{2}$.
又
∵$QB=DF$,$QE=EF$,
∴$EF^{2}=BE^{2}+DF^{2}=1+4=5$.
∴$EF=\sqrt {5}$(负值已舍去).
查看更多完整答案,请扫码查看


