《2025年诚成教育学业评价八年级物理下册人教版》

3.重为8N的物体挂在弹簧测力计下面，浸没到如图所示圆柱形容器的水中，此时弹簧测力计的示数为6N，已知容器底面积为100cm²，g取10N/kg，ρ水 =1.0×10³kg/m³。求:

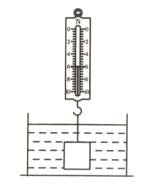
　(1)物体受到的浮力。
　
　(2)物体的密度。
　
　(3)物体浸没水中后，容器对水平桌面增大的压强。

答案： 解:
(1)$F_{浮}=G - F_{示}=8\text{ N}-6\text{ N}=2\text{ N}$
物体受到的浮力为$2\text{ N}$。
(2)$V_{物}=V_{排}=\frac{F_{浮}}{\rho_{水}g}$
$=\frac{2\text{ N}}{1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}}$
$= 2×10^{-4}\text{ m}^{3}$
$m_{物}=\frac{G}{g}=\frac{8\text{ N}}{10\text{ N/kg}} = 0.8\text{ kg}$
$\rho_{物}=\frac{m_{物}}{V_{物}}=\frac{0.8\text{ kg}}{2×10^{-4}\text{ m}^{3}} = 4×10^{3}\text{ kg/m}^{3}$
物体的密度为$4×10^{3}\text{ kg/m}^{3}$。
(3)$\Delta p=\frac{\Delta F}{S_{容}}=\frac{F_{浮}}{S_{容}}=\frac{2\text{ N}}{100×10^{-4}\text{ m}^{2}} = 200\text{ Pa}$
物体浸没水中后，容器对水平桌面增大的压强为$200\text{ Pa}$。

4.如图所示，水平地面上有一底面积为1.5×10⁻²m²的圆柱形薄壁容器，容器中水深40cm，一个边长为10cm的正方体物块通过一根细线与容器底部相连，细线受到的拉力为4N。(ρ水 =1.0×10³kg/m³，g取10N/kg)求:
　(1)此时容器底受到水的压强和压力。
　　
　(2)此时物块受到的浮力和物块的质量。
　
　(3)细线剪断后，物块静止时浸入水中的体积。

答案： 解:
(1)$h = 40\text{ cm}=0.4\text{ m}$
$p = \rho gh$
$= 1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}×0.4\text{ m}$
$= 4×10^{3}\text{ Pa}$
由$p = \frac{F}{S}$得
$F = pS = 4×10^{3}\text{ Pa}×1.5×10^{-2}\text{ m}^{2} = 60\text{ N}$
此时容器底受到水的压强为$4×10^{3}\text{ Pa}$，压力为$60\text{ N}$。
(2)$V = 0.1\text{ m}×0.1\text{ m}×0.1\text{ m}=1×10^{-3}\text{ m}^{3}$
$F_{浮}=\rho_{水}gV$
$= 1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}×1×10^{-3}\text{ m}^{3}$
$= 10\text{ N}$
$F_{浮}=F_{拉}+G$
$G = F_{浮}-F_{拉}=10\text{ N}-4\text{ N}=6\text{ N}$
由$G = mg$得
$m=\frac{G}{g}=\frac{6\text{ N}}{10\text{ N/kg}} = 0.6\text{ kg}$
此时物块受到的浮力为$10\text{ N}$，物块的质量为$0.6\text{ kg}$。
(3)细线剪断后，物块静止时处于漂浮状态
$F_{浮}'=G = 6\text{ N}$
由$F_{浮}=\rho_{液}gV_{排}$得
$V_{排}'=\frac{F_{浮}'}{\rho_{水}g}$
$=\frac{6\text{ N}}{1.0×10^{3}\text{ kg/m}^{3}×10\text{ N/kg}}$
$= 6×10^{-4}\text{ m}^{3}$
细线剪断后，物块静止时浸入水中的体积为$6×10^{-4}\text{ m}^{3}$。