《2025年诚成教育学业评价八年级物理下册人教版》

21.(学科素养·科学思维)在不计绳重及摩擦的情况下，请说出一点影响滑轮组机械效率的因素，并说明理由。

答案：
(1)在滑轮组一定的情况下，适当增加提升物体的重力，可提高滑轮组的机械效率。
理由:$\eta=\frac{W_{有用}}{W_{有用}+W_{额外}}=\frac{G_{物}h}{G_{物}h+G_{动}h}=\frac{1}{1+\frac{G_{动}}{G_{物}}}$
由机械效率公式可知，物重越大，效率越高。
(2)在物重一定的情况下，动滑轮越重，机械效率越低。
理由:$\eta=\frac{W_{有用}}{W_{有用}+W_{额外}}$，由公式可知，物重一定，有用功一定；动滑轮越重，额外功越多。所以，物重一定，动滑轮越重，机械效率越低。
(任选一点，合理即可)

22.(2024·绥化)如图甲所示，质量为40 kg的货物静止在水平地面上，与地面的接触面积是800 cm²。如图乙所示，工人用250 N的拉力F，将货物用滑轮组匀速提升到3 m高的二楼，此过程中货物上升的速度是0.2 m/s，g取10 N/kg。求：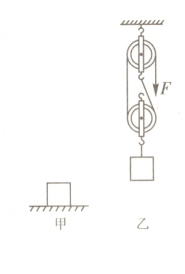
（1）货物静止在水平地面上时对地面的压强；
（2）工人用滑轮组提升货物时做功的功率；
（3）滑轮组的机械效率；
（4）为提高该滑轮组的机械效率，请你提出一条合理建议。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 解:
(1)因为货物静止在水平地面上
$F = G = mg = 40\ kg×10\ N/kg = 400\ N$
$S = 800\ cm^{2}=8×10^{-2}\ m^{2}$
货物对地面的压强
$p=\frac{F}{S}=\frac{400\ N}{8×10^{-2}\ m^{2}}=5×10^{3}\ Pa$
货物对地面的压强为$5×10^{3}\ Pa$。
(2)解法一:
绳子自由端移动的速度
$v = nv_{物}=2×0.2\ m/s = 0.4\ m/s$
工人做功的功率
$P=\frac{W}{t}=\frac{Fs}{t}=Fv = 250\ N×0.4\ m/s = 100\ W$
解法二:
绳子自由端移动的距离
$s = nh = 2×3\ m = 6\ m$
工人做的总功
$W_{总}=Fs = 250\ N×6\ m = 1500\ J$
绳子自由端移动的速度
$v = nv_{物}=2×0.2\ m/s = 0.4\ m/s$
货物上升的时间
$t=\frac{s}{v}=\frac{6\ m}{0.4\ m/s}=15\ s$或$t=\frac{h}{v_{物}}=\frac{3\ m}{0.2\ m/s}=15\ s$
工人做功的功率
$P=\frac{W_{总}}{t}=\frac{1500\ J}{15\ s}=100\ W$
工人做功的功率为100 W。
(3)解法一:
有用功
$W_{有用}=Gh = 400\ N×3\ m = 1200\ J$
绳子自由端移动的距离
$s = nh = 2×3\ m = 6\ m$
工人做的总功
$W_{总}=Fs = 250\ N×6\ m = 1500\ J$
机械效率
$\eta=\frac{W_{有用}}{W_{总}}=\frac{1200\ J}{1500\ J}=80\%$
解法二:
$\eta=\frac{W_{有用}}{W_{总}}=\frac{Gh}{Fs}=\frac{Gh}{Fnh}=\frac{G}{nF}=\frac{400\ N}{2×250\ N}=80\%$
解法三:
有用功
$W_{有用}=Gh = 400\ N×3\ m = 1200\ J$
货物上升的时间
$t=\frac{s}{v}=\frac{6\ m}{0.4\ m/s}=15\ s$或$t=\frac{h}{v_{物}}=\frac{3\ m}{0.2\ m/s}=15\ s$
工人做的总功
$W_{总}=Pt = 100\ W×15\ s = 1500\ J$
机械效率
$\eta=\frac{W_{有用}}{W_{总}}=\frac{1200\ J}{1500\ J}=80\%$
滑轮组的机械效率为80%。
(4)建议:①增加所提升的物重;
②减轻动滑轮重;
③减小摩擦或绳重。
(其他说法，表述正确即可给分)