《2025年高考冲刺优秀模拟试卷汇编45套数学》

1.已知全集U = R,集合A = {0,1,2,3},B = {−2,−1,0,1},则图中阴影部分表示的集合为

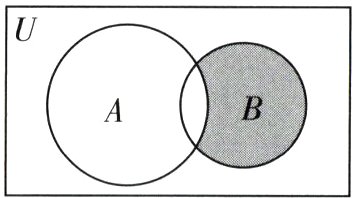
A. {−2,−1,0,1,2,3}
B. {0,1}
C. {2,3}
D. {−2,−1}

答案： 1.D　集合运算+韦恩图　设题图中阴影部分表示的集合的元素为x,则x∈B且x∉A,(题眼)又集合A = {0,1,2,3},B = {−2,−1,0,1},所以题图中阴影部分表示的集合为{−2,−1},故选D.

2.已知复数z满足iz = 1 + i,则$\overline{z}$ =
A. 1 + i
B. 1 - i
C. -1 + i
D. -1 - i

答案： 2.A　复数运算+共轭复数　由iz = 1 + i,得z = $\frac{1 + i}{i}$ = $\frac{(1 + i)×(-i)}{i×(-i)}$ = 1 - i,(题眼)所以$\overline{z}$ = 1 + i,故选A.

3.已知$\vec{a}$ = (3,λ),$\vec{b}$ = (1,2),若($\vec{a}$ - $\vec{b}$)⊥$\vec{b}$,则实数λ =
A. -4
B. 1
C. 2
D. 6

答案： 3.B　向量垂直+向量数量积的运算　解法一　坐标法　$\vec{a}$ - $\vec{b}$ = (2,λ - 2).因为($\vec{a}$ - $\vec{b}$)⊥$\vec{b}$,所以($\vec{a}$ - $\vec{b}$)·$\vec{b}$ = 2 + 2(λ - 2) = 0,(题眼)解得λ = 1,故选B.
解法二　坐标及向量综合法　因为($\vec{a}$ - $\vec{b}$)⊥$\vec{b}$,所以($\vec{a}$ - $\vec{b}$)·$\vec{b}$ = 0,即$\vec{a}$·$\vec{b}$ - $\vec{b}$² = 0,(题眼)所以3 + 2λ - (1² + 2²) = 0,解得λ = 1,故选B.

4.已知m,n是不同的直线,α,β是不同的平面,则下列说法中正确的是
A.若α//β,m⊂α,n⊂β,则m//n
B.若α//β,m//α,n//β,则m//n
C.若α⊥β,m⊥α,n⊥β,则m⊥n
D.若α⊥β,m//α,n//β,则m⊥n

答案： 4.C　空间中线面位置关系　对于A,若α//β,m⊂α,n⊂β,则m//n或m与n异面,所以A错误;
对于B,若α//β,m//α,n//β,则m//n或m与n异面或m与n相交，所以B错误;
对于C,设直线m,n的方向向量分别为$\vec{m}$,$\vec{n}$,因为m⊥α,n⊥β,所以$\vec{m}$⊥α,$\vec{n}$⊥β,即$\vec{m}$,$\vec{n}$分别为平面α，β的法向量，(题眼)又α⊥β,所以$\vec{m}$⊥$\vec{n}$,所以m⊥n,所以C正确;
对于D,若α⊥β,m//α,n//β,则m//n或m与n异面或m与n相交，所以m与n不一定垂直，所以D错误.综上，选C.

5.北斗七星是夜空中的七颗亮星,我国汉代纬书《春秋运斗枢》就有记载,它们组成的图形像我国古代舀酒的斗,故命名为北斗七星.北斗七星不仅是天上的星象,也是古人判断季节的依据之一.如图,用点A,B,C,D,E,F,G表示某季节的北斗七星,其中B,D,E,F看作共线,其他任何三点均不共线.若过这七个点中任意三个点作三角形，则所作的不同三角形的个数为

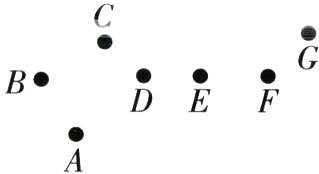
A. 30
B. 31
C. 34
D. 35

答案： 5.B　组合+分类加法、分步乘法计数原理解法一　排除法
从7个点中任意取3个点可构成$C_{7}^{3}$个三角形，因为B,D,E,F 四点共线，其中任意三点都不能构成三角形，(题眼)所以共可以构成$C_{7}^{3}-C_{4}^{3}$ = 35 - 4 = 31(个)不同三角形,故选B.
解法二　分类法　第一类:B,D,E,F四个点中一个点都不取,可构成$C_{3}^{3}$ = 1个三角形;第二类:从B,D,E,F四个点中取1个点,在A,C,G中取2个点,可构成$C_{4}^{1}C_{3}^{2}$ = 12个三角形;第三类:从B,D,E,F四个点中取2个点，在A,C,G中取1个点,可构成$C_{4}^{2}C_{3}^{1}$ = 18个三角形.共可以构成1 + 12 + 18 = 31(个)三角形,故选B.

6.已知双曲线$x^{2}-\frac{y^{2}}{3}=1$的左、右焦点分别是$F_1,F_2$,
限时120分钟 满分150分 答案见125页
点P在双曲线C上,且满足$\overrightarrow{F_1P}\cdot\overrightarrow{F_2P}=9$,则点P到双曲线C两条渐近线的距离之和为
A. $2\sqrt{2}$
B. 3
C. $2\sqrt{3}$
D. $2\sqrt{6}$

答案： 6.C　双曲线的定义+点到直线的距离+向量数量积运算+坐标法　由题意可知,$F_1$(-2,0),$F_2$(2,0),由双曲线的对称性，不妨设点P在双曲线的第一象限内，设P($x_0$,$y_0$),且$x_0$＞0,$y_0$＞0,则$\overrightarrow{F_1P}$ = ($x_0$ + 2,$y_0$),$\overrightarrow{F_2P}$ = ($x_0$ - 2,$y_0$).由$\overrightarrow{F_1P}\cdot\overrightarrow{F_2P}$ = 9,得$x_0^2$ - 4 + $y_0^2$ = 9,即$x_0^2$ + $y_0^2$ = 13　①.又点P在双曲线上,所以$x_0^2$ - $\frac{y_0^2}{3}$ = 1　②,由①②得$\begin{cases}x_0 = 2 \\ y_0 = 3 \end{cases}$,即P(2,3).(题眼)又双曲线$x^2 - \frac{y^2}{3} = 1$的渐近线方程为y = ±$\sqrt{3}$x,化为一般式为$\sqrt{3}$x - y = 0,$\sqrt{3}$x + y = 0,则点P(2,3)到两条渐近线的距离之和为$\frac{|2\sqrt{3} - 3|}{2}$ + $\frac{|2\sqrt{3} + 3|}{2}$ = 2$\sqrt{3}$,故选C.

7.已知数列$\{a_n\}$的前n项和为$S_n(n\in N^*)$,且满足$S_1 = 2,3S_n=(n + 2)a_n$,则使不等式$S_n＜2024$成立的n的最大值为
A. 15
B. 17
C. 20
D. 22

答案： 7.B　数列$\{a_n\}$中$S_n$与$a_n$的关系+累乘法求通项公式+验证法　因为3$S_n$ = (n + 2)$a_n$,则当n≥2时,3$S_n$ = (n + 2)($S_n$ - $S_{n - 1}$),化简得(n - 1)$S_n$ = (n + 2)$S_{n - 1}$,即$\frac{S_n}{S_{n - 1}}$ = $\frac{n + 2}{n - 1}$,所以当n≥2时,$\frac{S_n}{S_{n - 1}}$·$\frac{S_{n - 1}}{S_{n - 2}}$·$\frac{S_{n - 2}}{S_{n - 3}}$·$\frac{S_{n - 3}}{S_{n - 4}}$·$\frac{S_{n - 4}}{S_{n - 5}}$·$\frac{S_{n - 5}}{S_{n - 6}}$·...·$\frac{S_2}{S_1}$ = $\frac{4}{1}$×$\frac{5}{2}$×$\frac{6}{3}$×$\frac{7}{4}$×$\frac{8}{5}$×$\frac{9}{6}$×...×$\frac{n + 2}{n - 1}$,即$\frac{S_n}{S_1}$ = $\frac{n(n + 1)(n + 2)}{6}$.因为$S_1$ = 2,所以$S_n$ = $\frac{n(n + 1)(n + 2)}{3}$,(题眼)对n = 1也成立;易知$S_n$逐项递增且$S_{15}$ = $\frac{15×16×17}{3}$ = 1360,$S_{16}$ = $\frac{16×17×18}{3}$ = 1632,$S_{17}$ = $\frac{17×18×19}{3}$ = 1938,$S_{18}$ = $\frac{18×19×20}{3}$ = 2280,所以使不等式$S_n$＜2024成立的n的最大值为17,故选B.

8.已知$-\frac{\pi}{2}＜α＜0,-\pi＜β＜-\frac{\pi}{2}$,$\sin2α - \sinβ + \sin(2α + β)=0$,则下列结论正确的是
A. $\cosα - \cos\frac{β}{2}=0$
B. $\cosα + \sin\frac{β}{2}=0$
C. $\cos2α - \cosβ=0$
D. $\cos2α + \sinβ=0$

答案： 8.B　两角和的正弦公式+二倍角公式　第1步:对$\sin2α - \sinβ + \sin(2α + β)=0$变形
因为$\sin2α - \sinβ + \sin(2α + β)=0$,
所以$\sin2α - \sinβ + \sin2α\cosβ + \cos2α\sinβ=0$,
则$\sin2α(1 + \cosβ)=\sinβ(1 - \cos2α)$,即2$\sinα\cosα(1 + \cosβ)=2\sinβ\sin^2α$.因为$-\frac{\pi}{2}$＜α＜0,所以$\sinα$＜0,则$\cosα(1 + \cosβ)=\sinα\sinβ$,所以$\cosα\cosβ - \sinα\sinβ=-\cosα$,即$\cos(α + β)=\cos(α - \pi)$.
第2步:讨论角α + β,π - α的范围，确定角α与β的关系因为$-\frac{\pi}{2}$＜α＜0,$-\pi$＜β＜$-\frac{\pi}{2}$,所以$-\frac{3\pi}{2}$＜α + β＜$-\frac{\pi}{2}$,$-\frac{3\pi}{2}$＜α - π＜ - π,又$\cos(α + β)=\cos(α - \pi)$,所以α + β = α - π或α + β + α - π = - 2π.由α + β = α - π得β = - π,不符合题意,由α + β + α - π = - 2π,得2α = - β - π.(题眼)
第3步:根据角α与β的关系，确定选项
所以$\cos2α=\cos(-β - \pi)=\cos(β + \pi)=-\cosβ$,即$\cos2α + \cosβ=0$,所以选项C,D均错误
因为2α = - β - π,所以α = - $\frac{β}{2}$ - $\frac{\pi}{2}$,所以$\cosα=\cos(-\frac{β}{2} - \frac{\pi}{2})=\cos(\frac{β}{2} + \frac{\pi}{2})=-\sin\frac{β}{2}$,即$\cosα + \sin\frac{β}{2}=0$,故选项A错误，B正确.综上，选B.

9.下列结论正确的是
A.若随机变量X,Y满足Y = 2X - 1,则D(Y)= 2D(X) - 1
B.若随机变量$\xi$~$N(4,\sigma^{2})$,$P(\xi＜6)=0.82$,则$P(2＜\xi＜6)=0.64$
C.若样本相关系数r的绝对值越接近1,则成对样本数据的线性相关程度越强
D.记样本$x_1,x_2,\cdots,x_n$的平均数为$\overline{x}$,样本$y_1,y_2,\cdots,y_m$的平均数为$\overline{y}$($\overline{x}\neq\overline{y}$),若样本$x_1,x_2,\cdots,x_n,y_1,y_2,\cdots,y_m$的平均数为$\overline{z}=\frac{2}{5}\overline{x}+\frac{3}{5}\overline{y}$,则$\frac{n}{m}=\frac{2}{3}$

答案： 9.BCD　方差+正态分布+相关系数+平均数　对于A,若Y = 2X - 1,则D(Y)= 4D(X),所以选项A错误;
对于B,因为随机变量$\xi$~$N(4,\sigma^2)$,$P(\xi＜6)=0.82$,
所以$P(4＜\xi＜6)=P(\xi＜6)-P(\xi\leq4)=0.82 - 0.5 = 0.32$,因为$P(2＜\xi＜4)=P(4＜\xi＜6)$,(题眼)
所以$P(2＜\xi＜6)=2P(4＜\xi＜6)=0.64$,所以选项B正确;对于C,若样本相关系数r的绝对值越接近1,则成对样本数据的线性相关程度越强，所以选项C正确;
对于D,由题意可知$\overline{z}=\frac{n\overline{x}+m\overline{y}}{n + m}=\frac{2}{5}\overline{x}+\frac{3}{5}\overline{y}$,化简得(3n - 2m)$\overline{x}$=(3n - 2m)$\overline{y}$(题眼)因为$\overline{x}\neq\overline{y}$,所以3n - 2m = 0,即$\frac{n}{m}=\frac{2}{3}$,所以选项D正确.
综上，选BCD.

10.已知定义在R上的函数f(x)满足以下条件:①对于任意的x,y∈R,f(x + y)+f(x - y)=2f(x)f(y);②f(0)≠0;③f(k)=0,其中k是正常数.则下列结论正确的是
A.f(0)=1
B.f(2k)=1
C.f(x)是偶函数
D.f(x + 2k)+f(x)=0

答案： 10.ACD　抽象函数赋值法+函数奇偶性+函数求值
解法一　特殊函数法
因为$f(x + y) + f(x - y) = 2f(x)f(y)$，联想到函数$y = \cos x$（题眼），又$f(k) = 0$，所以构造函数$f(x) = \cos\frac{\pi}{2k}x$。所以有$f(0) = 1$，$f(2k) = -1$，$f(x)$是偶函数，$f(x + 2k) = \cos[\frac{\pi}{2k}(x + 2k)] = \cos(x + \pi) = -\cos x = -f(x)$，即$f(x + 2k) + f(x) = 0$。综上，选ACD。
解法二　赋值法
$f(x + y) + f(x - y) = 2f(x)f(y)$对任意$x,y\in R$都成立（题眼）。
对于A，令$x = y = 0$，得$2f(0) = 2f^{2}(0)$，因为$f(0) \neq 0$，所以$f(0) = 1$，所以选项A正确；
对于B，令$x = y = k$，得$f(2k) + f(0) = 2f^{2}(k)$，因为$f(0) = 1$，$f(k) = 0$，所以$f(2k) = -1$，所以选项B错误；
对于C，令$x = 0$，得$f(y) + f(-y) = 2f(0)f(y)$，因为$f(0) = 1$，所以$f(-y) = f(y)$，所以函数$f(x)$是偶函数，所以选项C正确；
对于D，令$y = k$，用$x + k$代换$x$，得$f(x + 2k) + f(x) = 2f(x + k)f(k)$，因为$f(k) = 0$，所以$f(x + 2k) + f(x) = 0$，所以选项D正确。
综上，选ACD。
考情速递　强化思维过程，突出对思维深度的考查
2023年新课标1卷第11题通过抽象函数考查赋值法、函数性质和函数极值等。本题也是通过抽象函数考查了赋值法与函数奇偶性，两题共性均是以抽象函数为背景，考法相似，强化思维过程，突出对思维深度的考查，体现以能力为重的考查理念，突出数学本质。