2025年高考冲刺优秀模拟试卷汇编45套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高考冲刺优秀模拟试卷汇编45套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
18.(17分)已知椭圆Γ:$\frac{x²}{a²}+\frac{y²}{b²}=1$(a>b>0)的左、右焦点分别是F₁,F₂,左、右顶点分别是A,B,离心率为$\frac{\sqrt{3}}{2}$,直线y=kx(k≠0)与椭圆交于M,N两点,四边形MF₁NF₂的周长为8,直线l(不经过点A,B)与Γ交于C,D两点.
(1)若以CD为直径的圆过点B,证明:l经过定点.
(2)若O为坐标原点,C,D关于x轴对称,且$\overrightarrow{OC}=2\overrightarrow{OE}$,$\overrightarrow{BC}=2\overrightarrow{BG}$,直线AE与Γ交于另一点K,证明:D,G,K三点共线.
(1)若以CD为直径的圆过点B,证明:l经过定点.
(2)若O为坐标原点,C,D关于x轴对称,且$\overrightarrow{OC}=2\overrightarrow{OE}$,$\overrightarrow{BC}=2\overrightarrow{BG}$,直线AE与Γ交于另一点K,证明:D,G,K三点共线.
答案:
椭圆的定义、方程、几何性质+直线与椭圆的位置关系+定点问题+三点共线问题
解:
(1)第1步:列方程,求椭圆T的标准方程
因为四边形MFNF的周长为8,离心率为$\frac{3}{2}$,
所以4a=8,$\frac{C}{a}$=$\frac{√3}{2}$,(提示:椭圆的定义的应用) (1分)
又a²=b²+c²,所以a=2,b=1, (2分)
故椭圆的标准方程为$\frac{x²}{4}$+y²=1. (3分)
第2步:设直线/的方程,与椭圆方程联立,得根与系数的关系由题意可知1的斜率不为0,(提示;:直线1的斜率为0时,BC
BD≠0)
故可设l的方程为x=my+n,C(x,y),D(x,y2),
联立,得 ,可得(m²+4)y²+2mny+n²−4=0,
,可得(m²+4)y²+2mny+n²−4=0,
(4分)
则△=(2mn)²−4(m²²+4)(n²−4)>0,即m²+4>n²,
y1+y2=−$\frac{2mn}{m²+4}$,y;y2=$\frac{n²−4}{m²+4}$ (5分)
第3步:根据以CD为直径的圆过点B得BC.BD=0,即可求得直线/过定点
易知B(2,0),
因为以CD为直径的圆过点B,所以BC.BD=0,
BC.BD=(x−2,y).(x−2,y2)=(my+n−2,y1).(my+n−2,y2)=(my1+n−2)(my2+n−2)+y;y2=(m²+1)yy2+m(n−2)(y+y2)+(n−2)²,则(m²+1)(n²−4)+m(n−2)(−2mn)+(n−2)²(m²+4)=0,
化简得(5n−6)(n−2)=0,解得n=$\frac{6}{5}$或n=2. (7分)
当n=2时,l:x=my+2过点B(2,0),不符合题意;
当n=$\frac{6}{5}$时,l:x=my+过6 定点($\frac{6}{5}$,0),满足题意
综上所述,直线I过定点($\frac{6}{5}$,0). (8分)
(2)第1步:设点C的坐标,进而得点D,E,G的坐标
不妨设C(s,t)(s≠±2),则D(s,−t),$\frac{s2}{4}$+t²=1,即4t²=4−s². (9分)
因为OC=2OE,BC=2BG,
所以E,G分别为线段OC,BC的中点,
所以E($\frac{S}{2}$,$\frac{t}{2}$),G($\frac{s+2}{2}$,$\frac{t}{2}$).(中点坐标公式的应用)(10分)
第2步:求直线AE的方程,并与椭圆方程联立,得点K的坐标易知直线AE的斜率存在且不为0,所以直线AE的方程为y= ,即y=$\frac{t}{s+4}$(x+2). (11分)
,即y=$\frac{t}{s+4}$(x+2). (11分)
由 ,得[1+$\frac{4t²}{(s+4)²}$]x²+$\frac{16t²}{(s+4)²}$x+$\frac{16t²}{(s+4)²}$-4=0,
,得[1+$\frac{4t²}{(s+4)²}$]x²+$\frac{16t²}{(s+4)²}$x+$\frac{16t²}{(s+4)²}$-4=0,
设K的坐标为(xk,yk),
 (13分)
(13分)
第3步:分别求kc,kpx,得kc=kp,即可得证
连接DG,DK,易知直线DG,DK的斜率均存在且均不为0,
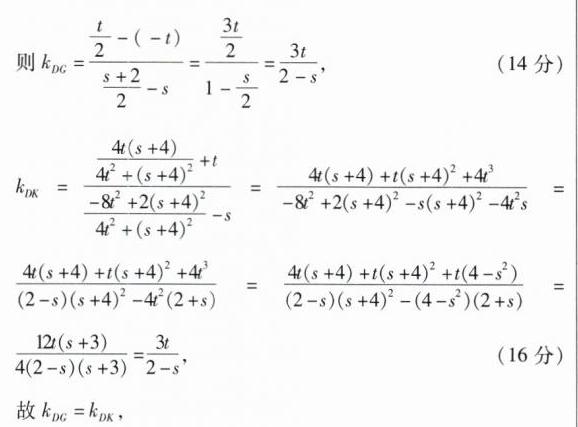
所以D,G,K三点共线.(提示:kDc=kD,且直线DG,DK均过点
D,故D,G,K三点共线) (17分)
延伸拓展 高考中解析几何解答题一般围绕直线与椭圆、直线与双曲线、直线与抛物线的位置关系进行设题,对考生的运算求解能力要求较高,挖掘几何图形的性质是求解有几何背景的圆锥曲线问题的主要思路.解决此类问题要做好两点:一是转化,把题中的已知和所求准确转化为代数中的数与式,即形向数的转化;二是设而不求,即联立直线方程与圆锥曲线的方程,利用根与系数的关系求解.
椭圆的定义、方程、几何性质+直线与椭圆的位置关系+定点问题+三点共线问题
解:
(1)第1步:列方程,求椭圆T的标准方程
因为四边形MFNF的周长为8,离心率为$\frac{3}{2}$,
所以4a=8,$\frac{C}{a}$=$\frac{√3}{2}$,(提示:椭圆的定义的应用) (1分)
又a²=b²+c²,所以a=2,b=1, (2分)
故椭圆的标准方程为$\frac{x²}{4}$+y²=1. (3分)
第2步:设直线/的方程,与椭圆方程联立,得根与系数的关系由题意可知1的斜率不为0,(提示;:直线1的斜率为0时,BC
BD≠0)
故可设l的方程为x=my+n,C(x,y),D(x,y2),
联立,得
 ,可得(m²+4)y²+2mny+n²−4=0,
,可得(m²+4)y²+2mny+n²−4=0,(4分)
则△=(2mn)²−4(m²²+4)(n²−4)>0,即m²+4>n²,
y1+y2=−$\frac{2mn}{m²+4}$,y;y2=$\frac{n²−4}{m²+4}$ (5分)
第3步:根据以CD为直径的圆过点B得BC.BD=0,即可求得直线/过定点
易知B(2,0),
因为以CD为直径的圆过点B,所以BC.BD=0,
BC.BD=(x−2,y).(x−2,y2)=(my+n−2,y1).(my+n−2,y2)=(my1+n−2)(my2+n−2)+y;y2=(m²+1)yy2+m(n−2)(y+y2)+(n−2)²,则(m²+1)(n²−4)+m(n−2)(−2mn)+(n−2)²(m²+4)=0,
化简得(5n−6)(n−2)=0,解得n=$\frac{6}{5}$或n=2. (7分)
当n=2时,l:x=my+2过点B(2,0),不符合题意;
当n=$\frac{6}{5}$时,l:x=my+过6 定点($\frac{6}{5}$,0),满足题意
综上所述,直线I过定点($\frac{6}{5}$,0). (8分)
(2)第1步:设点C的坐标,进而得点D,E,G的坐标
不妨设C(s,t)(s≠±2),则D(s,−t),$\frac{s2}{4}$+t²=1,即4t²=4−s². (9分)
因为OC=2OE,BC=2BG,
所以E,G分别为线段OC,BC的中点,
所以E($\frac{S}{2}$,$\frac{t}{2}$),G($\frac{s+2}{2}$,$\frac{t}{2}$).(中点坐标公式的应用)(10分)
第2步:求直线AE的方程,并与椭圆方程联立,得点K的坐标易知直线AE的斜率存在且不为0,所以直线AE的方程为y=
 ,即y=$\frac{t}{s+4}$(x+2). (11分)
,即y=$\frac{t}{s+4}$(x+2). (11分)由
 ,得[1+$\frac{4t²}{(s+4)²}$]x²+$\frac{16t²}{(s+4)²}$x+$\frac{16t²}{(s+4)²}$-4=0,
,得[1+$\frac{4t²}{(s+4)²}$]x²+$\frac{16t²}{(s+4)²}$x+$\frac{16t²}{(s+4)²}$-4=0,设K的坐标为(xk,yk),
 (13分)
(13分)第3步:分别求kc,kpx,得kc=kp,即可得证
连接DG,DK,易知直线DG,DK的斜率均存在且均不为0,
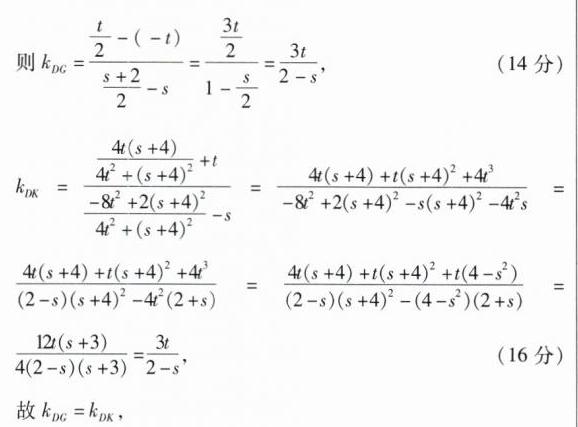
所以D,G,K三点共线.(提示:kDc=kD,且直线DG,DK均过点
D,故D,G,K三点共线) (17分)
延伸拓展 高考中解析几何解答题一般围绕直线与椭圆、直线与双曲线、直线与抛物线的位置关系进行设题,对考生的运算求解能力要求较高,挖掘几何图形的性质是求解有几何背景的圆锥曲线问题的主要思路.解决此类问题要做好两点:一是转化,把题中的已知和所求准确转化为代数中的数与式,即形向数的转化;二是设而不求,即联立直线方程与圆锥曲线的方程,利用根与系数的关系求解.
19.(17分)定义:若对于任意的n∈N*,数列{aₙ}满足aₙ₊₁ - aₙ>1,则称这个数列是“T数列”.
(1)已知首项为1的等差数列{aₙ}是“T数列”,且a₁ + a₂ + … + aₙ<n² + n恒成立,求a₂的取值范围.
(2)已知各项均为正整数的等比数列{aₙ}是“T数列”,数列{$\frac{aₙ}{2}$}不是“T数列”.记bₙ = $\frac{aₙ₊₁}{n}$,若数列{bₙ}是“T数列”.
①求数列{bₙ}的通项公式.
②是否存在正整数r,s,t(r<s<t),使$\frac{1}{bᵣ}$,$\frac{1}{bₛ}$,$\frac{1}{bₜ}$成等差数列?若存在,求出r,s,t的所有值;若不存在,请说明理由.
(1)已知首项为1的等差数列{aₙ}是“T数列”,且a₁ + a₂ + … + aₙ<n² + n恒成立,求a₂的取值范围.
(2)已知各项均为正整数的等比数列{aₙ}是“T数列”,数列{$\frac{aₙ}{2}$}不是“T数列”.记bₙ = $\frac{aₙ₊₁}{n}$,若数列{bₙ}是“T数列”.
①求数列{bₙ}的通项公式.
②是否存在正整数r,s,t(r<s<t),使$\frac{1}{bᵣ}$,$\frac{1}{bₛ}$,$\frac{1}{bₜ}$成等差数列?若存在,求出r,s,t的所有值;若不存在,请说明理由.
答案:
新定义“T数列”+等差数列的有关知识+与数列有关的不等式恒成立问题
解:
(1)第1步:根据“T数列”的定义得数列{an}的公差d>1 因为等差数列|an|是“T数列”,所以其公差d>1.
第2步:利用等差数列的前n项和公式化简原不等式,将问题转化
因为a=1,所以a1+a+.….+an=n+n(n2−1)d,(提示;等差数列的前n项和公式的应用) (1分)
由题意,得n+n(n2−1)d<n²+n对任意的n∈N恒成立,
即(n−1)d<2n对任意的n∈N.恒成立.
第3步:分类讨论,求d的范围
当n=1時,(n−1)d<2n恒成立,故d>1;
当n≥2时,(n−1)d<2n对任意的n∈N恒成立,即d<$\frac{2n}{n−1}$
对任意的neN.恒成立,(易错:没有讨论n是否等于1,直接将(n−1)d<2n转化为d<$\frac{2n}{n−1}$)
因为$\frac{2n}{n−1}$=2+$\frac{2}{n−1}$>2,所以d≤2.
综上,1<d≤2, (3分)
第4步:利用等差数列的通项公式求a的取值范围
所以2<a=1+d≤3,即a的取值范围是(2,3]. (4分)
(2)①第1步:分别求数列{an+1−a。},|$\frac{an+1}{2}$−$\frac{an}{2}$中的最小项
设等比数列{anI的公比为q,则a=aqn−,
因为“T数列”{a{的每一项均为正整数,所以q>1且q∈N.,
所以在数列an+1−an中,“a−α”为最小项,(点拨:可根据指数函数的图象与性质直接判断,也可由a+1−a>1得an+1>αm,进而根据q>1得an+1(g−1)>an(q−1),即a。+2−αn+1>an+1−α。,
从而得“a−a”为最小项)
在数列$\frac{an+1}{2}$−$\frac{a,}{2}${中,“$\frac{a}{2}$−$\frac{a,}{2}$”为最小项 (6分)
第2步:根据{an|是“T数列”,数列{$\frac{a,}{2}$|不是“T数列”求α1,9 的值
若a{是“T数列”,则只需a2−α1>1,即a(q−1)>1,
若数列$\frac{an}{2}$|不是“T数列”,则$\frac{a2}{2}$−$\frac{a}{2}$≤1,即a(q−1)≤2,
(7分)
因为数列|a{的每一项均为正整数,所以a(q−1)=2,
所以a=1,q=3或a=2,q=2. (8分)
第3步:分类讨论,分别检验数列{b。|是否为“T数列”,得结果
当a1=1,q=3时,a=3n−,则b=$\frac{3”}{n}$,
令c=bn+1−bn(n∈N'),则cn=$\frac{3+1}{n+1}$−$\frac{3”}{n}$=3”.$\frac{2n−1}{n(n+1)}$,
又cn+1−cn=3n+¹$\frac{2n+1}{(n+1)(n+2)}$−3”.$\frac{2n−1}{n(n+1)}$=$\frac{3"}{n+1}$.
$\frac{4n²+2}{n(n+2)}$>0,
所以{c。为递增数列,
又c=b2−b1=$\frac{9}{2}$−3=$\frac{3}{2}$>1,
所以对于任意的n∈N',都有c>1,即bn,−bn>1,
所以数列b{为“T数列”,符合题意 (9分)
当α1=2,q=2时,a=2。,则b=$\frac{2+1}{n}$
因为b2−b=$\frac{8}{2}$−4=0<1,所以数列bn不是“T数列”,不合题意
综上所述,数列|b|的通项公式为b。=$\frac{3”}{n}$.(提示:分类讨论后别忘了进行总结) (10分)
②第1步:根据题意得到关于r,s,t的方程
假设存在正整数r,s,(r<s<t),使$\frac{1}{6}$,$\frac{1}{b}$,$\frac{1}{b}$成等差数列,则$\frac{2}{b}$=$\frac{1}{6}$+$\frac{1}{6}$,即$\frac{2s}{3'}$=$\frac{r}{3′}$+$\frac{t}{3'}$ (11分)
第2步:判断$\frac{r}{3'}$,$\frac{s−1}{3−}$的大小关系
由于$\frac{n+1}{3+1}$−$\frac{n}{3”}$=$\frac{1−2n}{3=+1}$<0,所以数列$\frac{n}{3"}$为递减数列
因为r<s,所以r≤s−1且s至少为2,(提示:r,s,t(r<s<t)均为正整数)
所以$\frac{r}{3'}$≥$\frac{s−1}{3−1}$ (13分)
第3步:分类讨论,分别求得r,s,t的值,得结果
易知$\frac{s−1}{3'−1}$−$\frac{2s}{3}$=$\frac{s−3}{3'}$,
当s≥3时,$\frac{r}{3'}$≥$\frac{s−1}{3−1}$≥$\frac{2s}{3'}$,
又$\frac{t}{3'}$>0,所以$\frac{2s}{3'}$<$\frac{r}{3'}$+$\frac{t}{3}$,矛盾.(关键是找到矛盾) (15分)
当s=2时,r=1,所以$\frac{4}{9}$=$\frac{1}{3}$+$\frac{t}{3}$,即$\frac{t}{3'}$=$\frac{1}{9}$,
由于$\frac{n}{3”}$为递减数列,故$\frac{t}{3'}$=$\frac{1}{9}$有唯一解,即t=3.
综上,存在正整数r=1,s=2,t=3,使$\frac{1}{b}$,$\frac{1}{b}$,$\frac{1}{b}$成等差数列.
(17分)
方法技巧 破解新定义问题的攻略
(1)理解“新定义”,明确“新定义”的条件、原理、操作步骤和结论.
(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”,并归纳“举例”提供的解题方法.
(3)类比新定义的概念、原理、方法,解决问题
解:
(1)第1步:根据“T数列”的定义得数列{an}的公差d>1 因为等差数列|an|是“T数列”,所以其公差d>1.
第2步:利用等差数列的前n项和公式化简原不等式,将问题转化
因为a=1,所以a1+a+.….+an=n+n(n2−1)d,(提示;等差数列的前n项和公式的应用) (1分)
由题意,得n+n(n2−1)d<n²+n对任意的n∈N恒成立,
即(n−1)d<2n对任意的n∈N.恒成立.
第3步:分类讨论,求d的范围
当n=1時,(n−1)d<2n恒成立,故d>1;
当n≥2时,(n−1)d<2n对任意的n∈N恒成立,即d<$\frac{2n}{n−1}$
对任意的neN.恒成立,(易错:没有讨论n是否等于1,直接将(n−1)d<2n转化为d<$\frac{2n}{n−1}$)
因为$\frac{2n}{n−1}$=2+$\frac{2}{n−1}$>2,所以d≤2.
综上,1<d≤2, (3分)
第4步:利用等差数列的通项公式求a的取值范围
所以2<a=1+d≤3,即a的取值范围是(2,3]. (4分)
(2)①第1步:分别求数列{an+1−a。},|$\frac{an+1}{2}$−$\frac{an}{2}$中的最小项
设等比数列{anI的公比为q,则a=aqn−,
因为“T数列”{a{的每一项均为正整数,所以q>1且q∈N.,
所以在数列an+1−an中,“a−α”为最小项,(点拨:可根据指数函数的图象与性质直接判断,也可由a+1−a>1得an+1>αm,进而根据q>1得an+1(g−1)>an(q−1),即a。+2−αn+1>an+1−α。,
从而得“a−a”为最小项)
在数列$\frac{an+1}{2}$−$\frac{a,}{2}${中,“$\frac{a}{2}$−$\frac{a,}{2}$”为最小项 (6分)
第2步:根据{an|是“T数列”,数列{$\frac{a,}{2}$|不是“T数列”求α1,9 的值
若a{是“T数列”,则只需a2−α1>1,即a(q−1)>1,
若数列$\frac{an}{2}$|不是“T数列”,则$\frac{a2}{2}$−$\frac{a}{2}$≤1,即a(q−1)≤2,
(7分)
因为数列|a{的每一项均为正整数,所以a(q−1)=2,
所以a=1,q=3或a=2,q=2. (8分)
第3步:分类讨论,分别检验数列{b。|是否为“T数列”,得结果
当a1=1,q=3时,a=3n−,则b=$\frac{3”}{n}$,
令c=bn+1−bn(n∈N'),则cn=$\frac{3+1}{n+1}$−$\frac{3”}{n}$=3”.$\frac{2n−1}{n(n+1)}$,
又cn+1−cn=3n+¹$\frac{2n+1}{(n+1)(n+2)}$−3”.$\frac{2n−1}{n(n+1)}$=$\frac{3"}{n+1}$.
$\frac{4n²+2}{n(n+2)}$>0,
所以{c。为递增数列,
又c=b2−b1=$\frac{9}{2}$−3=$\frac{3}{2}$>1,
所以对于任意的n∈N',都有c>1,即bn,−bn>1,
所以数列b{为“T数列”,符合题意 (9分)
当α1=2,q=2时,a=2。,则b=$\frac{2+1}{n}$
因为b2−b=$\frac{8}{2}$−4=0<1,所以数列bn不是“T数列”,不合题意
综上所述,数列|b|的通项公式为b。=$\frac{3”}{n}$.(提示:分类讨论后别忘了进行总结) (10分)
②第1步:根据题意得到关于r,s,t的方程
假设存在正整数r,s,(r<s<t),使$\frac{1}{6}$,$\frac{1}{b}$,$\frac{1}{b}$成等差数列,则$\frac{2}{b}$=$\frac{1}{6}$+$\frac{1}{6}$,即$\frac{2s}{3'}$=$\frac{r}{3′}$+$\frac{t}{3'}$ (11分)
第2步:判断$\frac{r}{3'}$,$\frac{s−1}{3−}$的大小关系
由于$\frac{n+1}{3+1}$−$\frac{n}{3”}$=$\frac{1−2n}{3=+1}$<0,所以数列$\frac{n}{3"}$为递减数列
因为r<s,所以r≤s−1且s至少为2,(提示:r,s,t(r<s<t)均为正整数)
所以$\frac{r}{3'}$≥$\frac{s−1}{3−1}$ (13分)
第3步:分类讨论,分别求得r,s,t的值,得结果
易知$\frac{s−1}{3'−1}$−$\frac{2s}{3}$=$\frac{s−3}{3'}$,
当s≥3时,$\frac{r}{3'}$≥$\frac{s−1}{3−1}$≥$\frac{2s}{3'}$,
又$\frac{t}{3'}$>0,所以$\frac{2s}{3'}$<$\frac{r}{3'}$+$\frac{t}{3}$,矛盾.(关键是找到矛盾) (15分)
当s=2时,r=1,所以$\frac{4}{9}$=$\frac{1}{3}$+$\frac{t}{3}$,即$\frac{t}{3'}$=$\frac{1}{9}$,
由于$\frac{n}{3”}$为递减数列,故$\frac{t}{3'}$=$\frac{1}{9}$有唯一解,即t=3.
综上,存在正整数r=1,s=2,t=3,使$\frac{1}{b}$,$\frac{1}{b}$,$\frac{1}{b}$成等差数列.
(17分)
方法技巧 破解新定义问题的攻略
(1)理解“新定义”,明确“新定义”的条件、原理、操作步骤和结论.
(2)重视“举例”,利用“举例”检验是否理解和正确运用“新定义”,并归纳“举例”提供的解题方法.
(3)类比新定义的概念、原理、方法,解决问题
查看更多完整答案,请扫码查看


