《2025年高考冲刺优秀模拟试卷汇编45套数学》

1.已知平面向量$\vec{a}=(1,2)$，$\vec{b}=(-1,\lambda)$，若$\vec{a}\perp\vec{b}$，则实数$\lambda =$
A.$\frac{1}{2}$
B.$-\frac{1}{2}$
C.$-2$
D.$2$

答案： 1.A 向量的垂直 由$\vec{a} \perp \vec{b}$得$\vec{a} \cdot \vec{b} = -1 + 2\lambda = 0$，解得$\lambda = \frac{1}{2}$，故选A。

2.已知抛物线$C:x^{2}=y$上点$M$的纵坐标为$1$，则点$M$到$C$的焦点的距离为
A.$1$
B.$\frac{5}{4}$
C.$\frac{3}{2}$
D.$2$

答案： 2.B 抛物线的定义+抛物线的性质
解法一：定义法 抛物线$C$的准线方程为$y = -\frac{1}{4}$，点$M$到$C$的焦点的距离等于点$M$到$C$的准线的距离。因为点$M$的纵坐标为$1$，所以点$M$到准线$y = -\frac{1}{4}$的距离$d = 1 - (-\frac{1}{4}) = \frac{5}{4}$，故选B。
解法二：直接法 记抛物线$C$的焦点为$F$，则$F(0,\frac{1}{4})$。在$x^2 = y$中，令$y = 1$得$x = \pm1$，则$M(1,1)$或$M(-1,1)$，所以$|MF| = \sqrt{(0 \pm 1)^2 + (\frac{1}{4} - 1)^2} = \frac{5}{4}$，故选B。

3.已知集合$A=\{x|\log_{3}(2x + 1)=2\}$，集合$B=\{2,a\}$，其中$a\in R$。若$A\cup B = B$，则$a =$
A.$1$
B.$2$
C.$3$
D.$4$

答案： 3.D 集合的并运算+解对数方程
解法一：直接法 由$2x + 1 = 3^2$，得$x = 4$，所以$A = \{4\}$。由$A \cup B = B$，得$A \subseteq B$（题眼），所以$a = 4$，故选D。
解法二：排除法 由$2x + 1 = 3^2$，得$x = 4$，所以$A = \{4\}$。$a = 1$时，$A \cup B = \{1,2,4\} \neq B$，排除A；$a = 2$时不满足集合元素的互异性，排除B；$a = 3$时，$A \cup B = \{2,3,4\} \neq B$，排除C。故选D。

4.已知等差数列$\{a_{n}\}$的前$n$项和为$S_{n}$，$a_{1}=-1$，$S_{7}=5a_{4}+10$，则$S_{4}=$
A.$6$
B.$7$
C.$8$
D.$10$

答案： 4.C 等差数列的通项公式、前$n$项和公式+等差数列的性质
解法一：相关量法 设$\{a_n\}$的公差为$d$，由题知$S_7 = 7a_4 = 7(a_1 + 3d) = 5(a_1 + 3d) + 10$，解得$d = 2$（题眼），所以$S_4 = 4a_1 + 6d = 8$，故选C。
解法二：性质法 由题知$S_7 = 7a_4 = 5a_4 + 10$，解得$a_4 = 5$，所以$S_4 = \frac{4(a_1 + a_4)}{2} = \frac{(-1 + 5) \times 4}{2} = 8$，故选C。

5.12世纪以前的某时期，盛行欧洲的罗马数码采用简单累数制进行记数，现在一些场合还在使用，比如书本的卷数、老式表盘等。罗马数字用7个大写的拉丁文字母表示数目:
I V X L C D M
1 5 10 50 100 500 1000
例如：$58 = LVIII$，$464 = CCCC LXIV$。依据此记数方法，$MMXXXV =$
A.$2025$
B.$2035$
C.$2050$
D.$2055$

答案： 5.B 数学文化+阅读理解能力 由题知，简单累数制就是将每个字母所代表的数目相加，$M$代表$1000$，$X$代表$10$，$V$代表$5$，所以$MMXXXV = 1000 \times 2 + 10 \times 3 + 5 = 2035$，故选B。
考情速递：罗马数码背景 2022年全国甲卷（理科）第8题以《梦溪笔谈》中的“会圆术”为背景求弧长的近似值；2022年浙江卷第11题以“三斜求积”为背景求三角形的面积。数学文化渗透到高考题中，可以让学生了解数学文化，激发学生的学习兴趣和热情。本题以罗马数码为背景，考查学生的阅读理解能力。

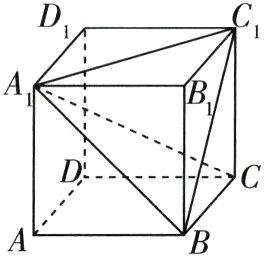
6.如图所示，在棱长为1的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中，点$P$为截面$A_{1}C_{1}B$上的动点，若$DP\perp A_{1}C$，则点$P$的轨迹长度是

A.$\frac{\sqrt{2}}{2}$
B.$\sqrt{2}$
C.$\frac{1}{2}$
D.$1$

答案： 6.B 立体几何中的轨迹问题+线面垂直的判定与性质 如图，连接$DC_1$，$D_1B$，$AC$，则$D_1B \perp AC$，$AA_1 \perp BD$，又$AA_1 \cap AC = A$，$AA_1$，$AC \subset$平面$AA_1C$，所以$BD \perp$平面$AA_1C$，又$AC_1 \subset$平面$AA_1C$，所以$BD \perp AC_1$，同理可得$BC_1 \perp AC_1$，又$BD \cap BC_1 = B$，$BD$，$BC_1 \subset$平面$BDC_1$，所以$AC_1 \perp$平面$BDC_1$。因为$AC_1 \perp DP$，所以$DP \subset$平面$BDC_1$，又$P \in$截面$A_1CB$，所以点$P$在平面$BDC_1$与截面$A_1CB$的交线段上，即点$P$的轨迹为线段$C_1B$，又$C_1B = \sqrt{2}$，所以点$P$的轨迹长度为$\sqrt{2}$，故选B。

7.已知数列$\{a_{n}\}$满足$a_{1}=0$，$a_{2}=1$。若数列$\{a_{n}+a_{n + 1}\}$是公比为2的等比数列，则$a_{2024}=$
A.$\frac{2^{2023}+1}{3}$
B.$\frac{2^{2024}+1}{3}$
C.$2^{1012}-1$
D.$2^{1011}-1$

答案： 7.A 等比数列的通项公式+数列的递推公式+累加法
解法一：累加法 由题知$a_1 + a_2 = 1$，所以$a_{n + 1} + a_n = 1\cdot2^{n - 1} = 2^{n - 1}$，所以$a_{n + 2} + a_{n + 1} = 2^n$，两式相减得$a_{n + 2} - a_n = 2^n - 2^{n - 1} = 2^{n - 1}$，所以$a_{2024} = a_2 + (a_4 - a_2) + (a_6 - a_4) + \cdots + (a_{2024} - a_{2022}) = 1 + 2^2 + 2^4 + \cdots + 2^{2022} = 1 + \frac{2^2(1 - 4^{1011})}{1 - 4} = 1 + \frac{2^{2023} - 2}{3} = \frac{2^{2023} + 1}{3}$，故选A。
解法二：构造数列法 由题知$a_1 + a_2 = 1$，所以$a_{n + 1} + a_n = 1\cdot2^{n - 1} = 2^{n - 1}$，所以$a_{n + 1} = -a_n + 2^{n - 1}$，$\frac{a_{n + 1}}{2^{n - 1}} = -\frac{a_n}{2^{n - 1}} + 1 = -\frac{1}{2}\cdot\frac{a_n}{2^{n - 2}} + 1$，$\frac{a_{n + 1}}{2^{n - 1}} - \frac{2}{3} = -\frac{1}{2}(\frac{a_n}{2^{n - 2}} - \frac{2}{3})$，所以$\{\frac{a_n}{2^{n - 2}} - \frac{2}{3}\}$是等比数列，$\frac{a_n}{2^{n - 2}} - \frac{2}{3} = (\frac{a_2}{2^0} - \frac{2}{3})\cdot(-\frac{1}{2})^{n - 1} = -\frac{2}{3}(-\frac{1}{2})^{n - 1}$，所以$a_n = 2^{n - 1} - \frac{2}{3}(1 - (-2)^{n - 1})$，因此$a_{2024} = 2^{2023} - \frac{2}{3}(1 - (-2)^{2023}) = \frac{2^{2023} + 1}{3}$，故选A。

8.已知直三棱柱$ABC - A_{1}B_{1}C_{1}$外接球的直径为6，且$AB\perp BC$，$BC = 2$，则该棱柱体积的最大值为
A.$8$
B.$12$
C.$16$
D.$24$

答案： 8.C 棱柱的外接球+棱柱体积的最值+基本不等式
教你审题
设$AB = a$，$AA_1 = h$。因为三棱柱为直三棱柱且$AB \perp BC$，所以可将其补形为一个长方体，如图，则该长方体的外接球即三棱柱$ABC - A_1B_1C_1$的外接球，所以外接球的直径为$\sqrt{a^2 + 2^2 + h^2} = 6$，所以$a^2 + h^2 = 32$。该三棱柱的体积$V = S_{\triangle ABC} \cdot h = \frac{1}{2} \cdot 2a \cdot h = ah \leq \frac{a^2 + h^2}{2} = 16$，当且仅当$a = h$时等号成立，故选C。

9.某次跳水比赛一共有八个评委现场打分，若八位评委给某个选手的打分分别为$x_{1},x_{2},\cdots,x_{8}$，记这组数据的平均数、中位数、方差、极差分别为$\overline{x},z,s^{2},j$；去掉这组数据的一个最高分和一个最低分后，其平均数、中位数、方差、极差分别为$\overline{x}',z',(s')^{2},j'$，则下列判断中一定正确的是
A.$\overline{x}\leq\overline{x}'$
B.$z = z'$
C.$(s')^{2}\leq s^{2}$
D.$j'\leq j$

答案： 9.BCD 平均数+中位数+方差+极差 根据平均数的性质可知，平均数受具体数值的影响，所以无法判断$\overline{x}_1$和$\overline{x}_2$的大小，故A不一定正确（举例：若这八个数据中，有一个数据是$90$，其他数据均是$80$，则显然选项A中的等式不成立）。根据中位数的定义可知，将这八个数据从小到大排列后，中间两个数据的平均数是中位数，去掉最大和最小的数据不影响中间两个数据，故B一定正确。根据方差的意义知，方差刻画了数据的波动程度，若这八个数据都相等，则去掉最大和最小的数据后，数据波动程度不变，若这八个数据不全相等，则去掉最大和最小的数据后，数据波动程度减小，故C一定正确。根据极差的定义知，若这八个数据都相等，则去掉最大和最小的数据后，剩余的数据的极差不变，若这八个数据不全相等，则去掉最大和最小的数据后，剩余的数据的极差减小，故D一定正确。故选BCD。

10.函数f(x)=2$\sqrt{3}$sinωxcosωx+2cos²ωx−1(0＜ω＜1)的图象如图所示,则
　
A.f(x)的最小正周期为2π
B.y=f(2x+$\frac{\pi}{3}$)是奇函数　
C.y=f(x+$\frac{\pi}{6}$)cosx的图象关于直线x=$\frac{\pi}{12}$对称
D.若y=f(tx)(t＞0)在[0,π]上有且仅有2个零点,则t∈[$\frac{11}{6}$,$\frac{17}{6}$)

答案： 10.ACD　二倍角公式+辅助角公式+三角函数的解析式+三角函数的性质(周期性、奇偶性、图象的对称性)　f(x)=√3sin2ωx + cos2ωx = 2sin(2ωx + $\frac{π}{6}$).由题图知x = $\frac{T}{3}$时f(x)取得最大值，所以sin(2ω·$\frac{T}{3}$ + $\frac{π}{6}$) = 1，得$\frac{2π}{3}$ω + $\frac{π}{6}$ = $\frac{π}{2}$ + 2kπ，k∈Z，ω = $\frac{1}{2}$ + 3k，k∈Z，因为0＜ω＜1，所以ω = $\frac{1}{2}$，f(x) = 2sin(x + $\frac{π}{6}$).
对于A，f(x)的最小正周期T = $\frac{2π}{1}$ = 2π，故A正确；
对于B，f(2x + $\frac{π}{3}$) = 2sin(2x + $\frac{π}{3}$ + $\frac{π}{6}$) = 2sin(2x + $\frac{π}{2}$) = 2cos2x，所以y = f(2x + $\frac{π}{3}$)是偶函数，故B错误；
对于C，f(x + $\frac{π}{6}$)cosx = 2sin(x + $\frac{π}{3}$)cosx = (sinx + √3cosx)cosx = sinxcosx + √3cos²x = $\frac{1}{2}$sin2x + √3×$\frac{1 + cos2x}{2}$ = sin(2x + $\frac{π}{3}$) + $\frac{\sqrt{3}}{2}$，当x = $\frac{π}{12}$时，2x + $\frac{π}{3}$ = $\frac{π}{2}$，所以y = f(x + $\frac{π}{6}$)cosx的图象关于直线x = $\frac{π}{12}$对称，故C正确；
对于D，f(tx) = 2sin(tx + $\frac{π}{6}$)，当x∈[0,π]时，tx + $\frac{π}{6}$∈[$\frac{π}{6}$,tπ + $\frac{π}{6}$]，结合y = sinx的图象知，若y = f(tx)(t＞0)在[0,π]上有且仅有2个零点，则tπ + $\frac{π}{6}$∈[2π,3π)，得t∈[$\frac{11}{6}$,$\frac{17}{6}$)，故D正确.综上，选ACD.

11.已知函数f(x)及其导函数f'(x)的定义域均为R,记g(x)=f'(x),且f(x)−f(−x)=2x,g(x)+g(2−x)=0,则
　
A.g(0)=1
　
B.y=$\frac{f(x)}{x}$的图象关于点(0,1)对称
　
C.f(x)+f(2−x)=0

D.$\sum_{k = 1}^{n}kg(k)=\frac{n(n - 1)}{2}$(n∈N*)

答案： 11.ABD　抽象函数求导+函数图象的对称性+等差数列的定义+赋值法　对f(x)−f(−x) = 2x的两边同时求导，得f'(x) + f'(−x) = 2，所以g(x) + g(−x) = 2①.
对于A，在①中令x = 0，得g
(0) + g
(0) = 2，解得g
(0) = 1，故A正确；
对于B，$\frac{f(x)}{x}$ + $\frac{f(−x)}{−x}$ = $\frac{f(x) - f(−x)}{x}$ = $\frac{2x}{x}$ = 2，所以y = $\frac{f(x)}{x}$的图象关于点(0,1)对称，故B正确；
对于C，假设f(x) + f(2−x) = 0成立，对其两边同时求导得f'(x)−f'(2−x) = 0，所以g(x)−g(2−x) = 0，又g(x) + g(2−x) = 0，所以g(x) = 0，与g
(0) = 1矛盾，故C错误；
对于D，g(x) + g(2−x) = 0，g(x) + g(−x) = 2，两式相减得g(−x)−g(2−x) = 2，所以g(x)−g(2 + x) = 2，可知数列{g(n)}所有奇数项成公差为−2的等差数列，所有偶数项成公差为−2的等差数列.在g(x) + g(2−x) = 0中，令x = 0，得g
(0) + g
(2) = 0，令x = 1，得2g
(1) = 0，所以g
(1) = 0，g
(2) = −1，所以{g(n)}是首项为0，公差为−1的等差数列，所以g(n) = −n + 1，所以$\sum_{k = 1}^{n}g(k)$ = $\frac{n(0 - n + 1)}{2}$ = $\frac{n - n²}{2}$，故D正确.综上，选ABD.
考情速递　关注热点.抽象函数问题　抽象函数问题是高考的热点，2023年新课标1卷第11题，2022年新高考I卷第12题，2022年新高考II卷第8题，均考查抽象函数问题.这类问题的核心是赋值，既可以用常数赋值，也可以用变量赋值，对学生的综合能力要求较高.
延伸拓展　抽象函数问题与方法总结
(1)求值:赋值法，将0,±1,±2等特殊值代入求值.
(2)单调性:对式子变形构造出f(x₁)−f(x₂)，利用单调性的定义，判断函数的单调性.
(3)奇偶性:构造f(−x)与f(x)的关系式，判断函数的奇偶性.
(4)对称性:构造f(a±x)与f(x)的关系式，判断函数的对称性.
(5)周期性:构造f(x + T)与f(x)的关系式，判断函数的周期性.
(6)与导数结合:对等式两边同时求导得出所需结论.
常见的抽象函数模型
f(x + y) = f(x) + f(y)，构造正比例函数f(x) = kx；
f(x + y) = f(x)f(y)，构造指数函数f(x) = aˣ；
f(xy) = f(x) + f(y)，构造对数函数f(x) = logₐx；
f(xy) = f(x)f(y)，构造幂函数f(x) = xⁿ.