2025年高考冲刺优秀模拟试卷汇编45套数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年高考冲刺优秀模拟试卷汇编45套数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
1.已知集合A = {−1, 0, 1, 2},B = {x|x² = x},则A∩B =
A. {−1}
B. {−1, 1}
C. {0, 1}
D. {−1, 0, 1}
A. {−1}
B. {−1, 1}
C. {0, 1}
D. {−1, 0, 1}
答案:
1.D 集合的交集 因为A=I−1,0,1,2},B=|x1x²=x}=
|−1,0,1{,所以A∩B=−1,0,1{,故选D.
|−1,0,1{,所以A∩B=−1,0,1{,故选D.
2.在下列各组向量中,可以作为基底的是
A. e₁ = (0, 0),e₂ = (1, −2)
B. e₁ = (−1, 2),e₂ = (5, 7)
C. e₁ = (3, 5),e₂ = (6, 10)
D. e₁ = (2, −3),e₂ = ($\frac{1}{2}$, −$\frac{3}{4}$)
A. e₁ = (0, 0),e₂ = (1, −2)
B. e₁ = (−1, 2),e₂ = (5, 7)
C. e₁ = (3, 5),e₂ = (6, 10)
D. e₁ = (2, −3),e₂ = ($\frac{1}{2}$, −$\frac{3}{4}$)
答案:
2.B 基底的概念 若两向量不共线,则这两个向量可以作为基底:(题眼)对于A,e1=(0,0),e2=(1,−2),因为e、//e2,所以e;,e2不能作为基底;对于B,e=(−1,2),e2=(5,7),因为−1x7≠2xs,所以e1,e2不共线,所以e1,e2可以作为基底;对于C,e=(3,5),e2=(6,10),因为e//e2,所以e,e2不能作为基底;对于D,e=(2,−3),e22=($\frac{1}{2}$,−$\frac{3}{4}$),因为e//e2,所以e,e2不能作为基底.综上,选B.
3.已知复数z₁,z₂满足|z₁| = |z₂| = 3,z₁ + z₂ = 2 − $\sqrt{5}$i,则|z₁ − z₂| =
A. 3
B. 2$\sqrt{3}$
C. 3$\sqrt{2}$
D. 3$\sqrt{3}$
A. 3
B. 2$\sqrt{3}$
C. 3$\sqrt{2}$
D. 3$\sqrt{3}$
答案:
3.D 复数加减法的几何意义+向量的模+向量的数量积解法一 向量法 设复数z,对应的向量分别为0z,oz,复数z1+2对应的向量为0z,则oz=0Z+0Z.因为z+z2=
2−√5i,所以1021=3,即10歹;+0Z1=3.又1z1=1221=3,所以IOZ,1=10Z;1=3.因为复数z−2对应的向量为OZ,−0Z;,所以求lz1−221,即求10Z−0Z;1.(题眼)因为10Z;+oZ;1=3,平方得OZ²+0Z²+2OZ.0Z=9,所以2oZ.0Z;=−9,所以10Z−0Z21²=0Z²+0Z²−20Z;.0Z=9+9+9=27,所以10Z−0Z1=3√3,即1z1−21=3、√3,故选D.
解法二 数形结合法 设复数z,22对应
的向量分别为0z,0Z,复数z1+z对应
 的向量为02,则oz=0Z;+0Z2.因为z+
的向量为02,则oz=0Z;+0Z2.因为z+
2=2−$\sqrt{5}$i,所以10z1=3,即1oZ+oz;1=3.作出向量oZ,0Z;及向量Oz,如图所示,因为Oz=OZ;+OZ2,所以四边形OZZ忍为平行四边形,又1oZ;1=10Z1=1021=3,所以△0ZZ是边长为3 的正三角形,则∠ZρZ=120°,在△0ZZ2中,由余弦定理得1221= $\sqrt{0Z,1²+10Z1²−210Z,1.10Zlos120°}$=3√3,因为复数z−2对应的向量为OZ;−0Z=歹Z,所以1z−;1=
1ZZ1=3、√3,故选D.
3.D 复数加减法的几何意义+向量的模+向量的数量积解法一 向量法 设复数z,对应的向量分别为0z,oz,复数z1+2对应的向量为0z,则oz=0Z+0Z.因为z+z2=
2−√5i,所以1021=3,即10歹;+0Z1=3.又1z1=1221=3,所以IOZ,1=10Z;1=3.因为复数z−2对应的向量为OZ,−0Z;,所以求lz1−221,即求10Z−0Z;1.(题眼)因为10Z;+oZ;1=3,平方得OZ²+0Z²+2OZ.0Z=9,所以2oZ.0Z;=−9,所以10Z−0Z21²=0Z²+0Z²−20Z;.0Z=9+9+9=27,所以10Z−0Z1=3√3,即1z1−21=3、√3,故选D.
解法二 数形结合法 设复数z,22对应
的向量分别为0z,0Z,复数z1+z对应
 的向量为02,则oz=0Z;+0Z2.因为z+
的向量为02,则oz=0Z;+0Z2.因为z+2=2−$\sqrt{5}$i,所以10z1=3,即1oZ+oz;1=3.作出向量oZ,0Z;及向量Oz,如图所示,因为Oz=OZ;+OZ2,所以四边形OZZ忍为平行四边形,又1oZ;1=10Z1=1021=3,所以△0ZZ是边长为3 的正三角形,则∠ZρZ=120°,在△0ZZ2中,由余弦定理得1221= $\sqrt{0Z,1²+10Z1²−210Z,1.10Zlos120°}$=3√3,因为复数z−2对应的向量为OZ;−0Z=歹Z,所以1z−;1=
1ZZ1=3、√3,故选D.
4.酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定:100mL血液中酒精含量大于或者等于20mg,小于80mg认定为饮酒驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到了0.6mg/mL.如果停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过几个小时才能驾驶?(结果取整数,参考数据:lg3 ≈ 0.48,lg7 ≈ 0.85)
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
4.D 指数运算+对数运算设至少经过n(n∈N')个小时才能驾驶,则有60×(1−30%)”<20,即0.7”<$\frac{1}{3}$,(题眼)两边同时取对数得lg0.7"<lg$\frac{1}{3}$,即nlg0.7<lg$\frac{1}{3}$,因为lg0.7<0,所以n>$\frac{1g3}{lg0.7}$$\frac{1}{3}$=1g3−=−lg71−gl3g10≈$\frac{−0.48}{0.85−1}$=3.2,所以1g$\frac{7}{10}$
n≥4,即至少经过4个小时才能驾驶,故选D.
考情速递 以社会热点酒驾为情境 2023年新课标I卷第
10题以噪声污染问题为背景考查对数运算,本题以酒驾问
题为背景考查指数和对数运算.两题的共性是以考生熟悉的
社会热点问题为情境,既体现了数学的应用性,又引导了同
学们用数学知识思考问题
n≥4,即至少经过4个小时才能驾驶,故选D.
考情速递 以社会热点酒驾为情境 2023年新课标I卷第
10题以噪声污染问题为背景考查对数运算,本题以酒驾问
题为背景考查指数和对数运算.两题的共性是以考生熟悉的
社会热点问题为情境,既体现了数学的应用性,又引导了同
学们用数学知识思考问题
5.已知函数f(x) = 3log₂($\sqrt{x² + 1}$ − x),正数a,b满足f(a) + f(3b − 1) = 0,则$\frac{3b + a}{ab}$的最小值为
A. 6
B. 8
C. 12
D. 24
A. 6
B. 8
C. 12
D. 24
答案:
5.C 函数的奇偶性、单调性+基本不等式+整体代换法 因
为 $\sqrt{x²+1}$−x> $\sqrt{x2}$−x=1xl−x≥0,所以函数∮(x)=
3log2( $\sqrt{x²+1}$−x)的定义域为R.又∮(−x)=3log2( $\sqrt{x²+1}$+
x)=3log2[(√x²+1[(√x²+1+x)(√x²+1−x)]=31$\sqrt{x²+1}$+x)(√x²+1−x)]=31og2($\frac{1}{²+1}$)=
−31og2( $\sqrt{x²+1}$−x)=−∮(x),所以函数f(x)是奇函数.令t=
$\sqrt{x²+1}$−x=$\sqrt{x²+1}$1+x,当x≥0时,y= $\sqrt{x²+1}$,y=x均为单
调递增函数,所以t= $\sqrt{x²+1}$−x=$\frac{1}{+1+}$在[0,+x)上单调递减,所以函数∮(x)=3log2( $\sqrt{x²+1}$−x)在[0,+∞)上单调递减,又函数f(x)是奇函数,所以函数∮(x)=3log2( $\sqrt{x²+1}$−x)
在R上单调递减.因为f(a)+f(3b−1)=0,所以f(a)=
−∮(3b−1)=f(1−3b),所以a=1−3b,即a+3b=1.(题眼)又a,b均为正数,所以$\frac{3b+a}{ab}$=$\frac{3}{a}$+$\frac{1}{6}$=($\frac{3}{a}$+$\frac{1}{b}$)(a+3b)=6+
$\frac{96}{a}$+$\frac{a}{b}$≥6+2 $\sqrt{\frac{96}{a}\frac{a}{b}}$ 12,当且仅当$\frac{96}{a}$=$\frac{a}{b}$时等号成立,
又a+3b=1,所以a=$\frac{1}{2}$,b=$\frac{1}{6}$时等号成立,所以$\frac{3b+a}{ab}$的最小值为12,故选C.(另解:因为a+3b=1,所以$\frac{3b+a}{ab}$=$\frac{1}{ab}$=$\frac{3}{a.3b}$≥$\frac{3}{a+3b、²}$ 3 12,当且仅当α=3b时等号成立,又a+3b=1,所以$\frac{a+3b}{2}$ $\frac{1}{4}$
a=$\frac{1}{2}$,b=$\frac{1}{6}$时等号成立,所以$\frac{3b+a}{ab}$的最小值为12,故选C)
为 $\sqrt{x²+1}$−x> $\sqrt{x2}$−x=1xl−x≥0,所以函数∮(x)=
3log2( $\sqrt{x²+1}$−x)的定义域为R.又∮(−x)=3log2( $\sqrt{x²+1}$+
x)=3log2[(√x²+1[(√x²+1+x)(√x²+1−x)]=31$\sqrt{x²+1}$+x)(√x²+1−x)]=31og2($\frac{1}{²+1}$)=
−31og2( $\sqrt{x²+1}$−x)=−∮(x),所以函数f(x)是奇函数.令t=
$\sqrt{x²+1}$−x=$\sqrt{x²+1}$1+x,当x≥0时,y= $\sqrt{x²+1}$,y=x均为单
调递增函数,所以t= $\sqrt{x²+1}$−x=$\frac{1}{+1+}$在[0,+x)上单调递减,所以函数∮(x)=3log2( $\sqrt{x²+1}$−x)在[0,+∞)上单调递减,又函数f(x)是奇函数,所以函数∮(x)=3log2( $\sqrt{x²+1}$−x)
在R上单调递减.因为f(a)+f(3b−1)=0,所以f(a)=
−∮(3b−1)=f(1−3b),所以a=1−3b,即a+3b=1.(题眼)又a,b均为正数,所以$\frac{3b+a}{ab}$=$\frac{3}{a}$+$\frac{1}{6}$=($\frac{3}{a}$+$\frac{1}{b}$)(a+3b)=6+
$\frac{96}{a}$+$\frac{a}{b}$≥6+2 $\sqrt{\frac{96}{a}\frac{a}{b}}$ 12,当且仅当$\frac{96}{a}$=$\frac{a}{b}$时等号成立,
又a+3b=1,所以a=$\frac{1}{2}$,b=$\frac{1}{6}$时等号成立,所以$\frac{3b+a}{ab}$的最小值为12,故选C.(另解:因为a+3b=1,所以$\frac{3b+a}{ab}$=$\frac{1}{ab}$=$\frac{3}{a.3b}$≥$\frac{3}{a+3b、²}$ 3 12,当且仅当α=3b时等号成立,又a+3b=1,所以$\frac{a+3b}{2}$ $\frac{1}{4}$
a=$\frac{1}{2}$,b=$\frac{1}{6}$时等号成立,所以$\frac{3b+a}{ab}$的最小值为12,故选C)
6.为了迎接2025年第九届亚冬会的召开,某班组织全班学生开展有关亚冬会知识的竞赛活动.已知该班男生35人,女生25人.根据统计分析,男生组成绩和女生组成绩的方差分别为s₁²,s₂²,该班成绩的方差为s²,则下列结论中一定正确的是
2024年东北三省四市教研联合体高考模拟(一)
数学 - 限时120分钟 满分150分 答案见106页
A. s² = $\frac{s₁² + s₂²}{2}$
B. s² ≥ $\frac{s₁² + s₂²}{2}$
C. s² = $\frac{7s₁² + 5s₂²}{12}$
D. s² ≥ $\frac{7s₁² + 5s₂²}{12}$
2024年东北三省四市教研联合体高考模拟(一)
数学 - 限时120分钟 满分150分 答案见106页
A. s² = $\frac{s₁² + s₂²}{2}$
B. s² ≥ $\frac{s₁² + s₂²}{2}$
C. s² = $\frac{7s₁² + 5s₂²}{12}$
D. s² ≥ $\frac{7s₁² + 5s₂²}{12}$
答案:
6.D 总体方差与各层方差的关系 设该班的男生组成绩的平均值为x,女生组成绩的平均值为歹,该班成绩的平均值为z.
因为男生组成绩和女生组成绩的方差分别为S;,,该班成绩的方差为s²,且男生有35人,女生有25人,所以x=
35s;+25S²+353(5x+−25))²+25(y−z))²≥$\frac{35s²+25s2}{60}$=$\frac{7s²+5s2}{12}$,故选D.
知识积累 总体的方差
若一个总体分为二层,第一层的样本个数为m,平均值为x 方差为s;;第二层的样本个数为n,平均值为y,方差为s2;总体平均值为 三,方差为 s². 则 =m+ny ²=ms²+ns²+m(x−z)²+n(y−=)².
m+n
证明:设第一层的个体分别为x;,x2,x3,...,xm,第二层的个体分别为y,y2,y3,...,yn,
则x=x+x+x+...+xm=y+y²+yn+…..+yn,
即x+x2+x3+.….+xm=mx,y+y2+y3+...+y=ny;
所以=x−+x²+x+…..+xm+y+y+y³³+…..+y=mxm++nnny.因为=(x−x))²+(x−x)²+(x³−x))²+...+(xm−x)²,m
即(x−x)²+(x2−x)²+(x3−x)²+...+(xm−x)²=ms²,s²=(y−y)²+(y−y)²+(ny3−y))²+...+(yn−y)²,
即(y1−)²+(y2−y)²+(y3−y)²+...+(yn−y)²=ns²,所以s²=
(x−=)²+(x−=)²+...+(xm−=)²+Gy−=)²+(y2−)²+...+(y−三)²m+n
m+n
(xi−x)²+m(x−z)²+((y−)²+n(y−=)²
m+n =
$\frac{ms²+ns²+m(x−)²+n(y−z)²}{m+n}$
因为男生组成绩和女生组成绩的方差分别为S;,,该班成绩的方差为s²,且男生有35人,女生有25人,所以x=
35s;+25S²+353(5x+−25))²+25(y−z))²≥$\frac{35s²+25s2}{60}$=$\frac{7s²+5s2}{12}$,故选D.
知识积累 总体的方差
若一个总体分为二层,第一层的样本个数为m,平均值为x 方差为s;;第二层的样本个数为n,平均值为y,方差为s2;总体平均值为 三,方差为 s². 则 =m+ny ²=ms²+ns²+m(x−z)²+n(y−=)².
m+n
证明:设第一层的个体分别为x;,x2,x3,...,xm,第二层的个体分别为y,y2,y3,...,yn,
则x=x+x+x+...+xm=y+y²+yn+…..+yn,
即x+x2+x3+.….+xm=mx,y+y2+y3+...+y=ny;
所以=x−+x²+x+…..+xm+y+y+y³³+…..+y=mxm++nnny.因为=(x−x))²+(x−x)²+(x³−x))²+...+(xm−x)²,m
即(x−x)²+(x2−x)²+(x3−x)²+...+(xm−x)²=ms²,s²=(y−y)²+(y−y)²+(ny3−y))²+...+(yn−y)²,
即(y1−)²+(y2−y)²+(y3−y)²+...+(yn−y)²=ns²,所以s²=
(x−=)²+(x−=)²+...+(xm−=)²+Gy−=)²+(y2−)²+...+(y−三)²m+n
m+n
(xi−x)²+m(x−z)²+((y−)²+n(y−=)²
m+n =
$\frac{ms²+ns²+m(x−)²+n(y−z)²}{m+n}$
7.甲、乙、丙三人从事a,b,c三项工作,乙的年龄比从事c工作人的年龄大,丙的年龄与从事b工作人的年龄不同,从事b工作人的年龄比甲的年龄小,则甲、乙、丙的职业分别是
A. a,b,c
B. c,a,b
C. c,b,a
D. b,c,a
A. a,b,c
B. c,a,b
C. c,b,a
D. b,c,a
答案:
7.A 逻辑推理 列表法 首先作一个如下的表格:

因为乙的年龄比从事c工作人的年龄大,所以乙没有从事c工作;因为丙的年龄与从事b工作人的年龄不同,所以丙没有从事b工作;因为从事b工作人的年龄比甲的年龄小,所以甲没有从事b工作
得到下表:

由表可知,乙从事b工作,得到下表:
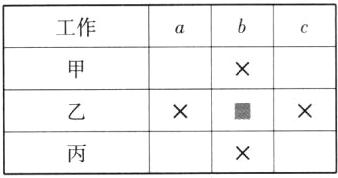
假设甲从事c工作,则丙从事a工作,得到下表:

由乙的年龄比从事c工作人的年龄大,得乙的年龄大于甲的年龄;由从事b工作人的年龄比甲的年龄小,得乙的年龄小于甲的年龄,所以矛盾,故假设不成立.所以甲从事a工作,丙从事c 工作,故选A.
7.A 逻辑推理 列表法 首先作一个如下的表格:

因为乙的年龄比从事c工作人的年龄大,所以乙没有从事c工作;因为丙的年龄与从事b工作人的年龄不同,所以丙没有从事b工作;因为从事b工作人的年龄比甲的年龄小,所以甲没有从事b工作
得到下表:

由表可知,乙从事b工作,得到下表:

假设甲从事c工作,则丙从事a工作,得到下表:

由乙的年龄比从事c工作人的年龄大,得乙的年龄大于甲的年龄;由从事b工作人的年龄比甲的年龄小,得乙的年龄小于甲的年龄,所以矛盾,故假设不成立.所以甲从事a工作,丙从事c 工作,故选A.
8.在同一平面直角坐标系内,函数y = f(x)及其导函数y = f'(x)的图象如图所示,已知两图象有且仅有一个公共点,其坐标为(0, 1),则

A. 函数y = f(x)·eˣ的最大值为1
B. 函数y = f(x)·eˣ的最小值为1
C. 函数y = $\frac{f(x)}{e^x}$的最大值为1
D. 函数y = $\frac{f(x)}{e^x}$的最小值为1

A. 函数y = f(x)·eˣ的最大值为1
B. 函数y = f(x)·eˣ的最小值为1
C. 函数y = $\frac{f(x)}{e^x}$的最大值为1
D. 函数y = $\frac{f(x)}{e^x}$的最小值为1
答案:
8.C 利用导数研究函数的单调性和最值+看图、识图、用图
第1步:确定A(x)的图象和f'(x)的图象
若虚线是函数f(x)的图象,实线是函数f'(x)的图象,则函数f(x)有增有减,则f'(x)有正有负,与题图不符,所以实线是函数∮(x)的图象,虚线是函数f'(x)的图象.由题图可知∮
(0)=
1∮'
(0)=1,f,(x)≥0恒成立,所以函数f(x)在R上单调递增,且∮(x)≥0恒成立.(题眼)
第2步:研究函数y=f(x).e;的最值
因为y=∮(x).e²,所以y'=e²(A(x)+f−(x))≥0恒成立,所以函数y=f(x).e在R上单调递增,所以函数y=f(x).e²无最值第3步:研究函数y=八的最值
因为y=,所以y、=∠(x)|f(x)当x>0时,由题图可知∮(x)>f'(x),所以y'<0;当x<0时,由题图可知,f'(x)>f(x),所以y,>0.所以函数y=在(−∞,,0)上单调递增,在(0',+∞))上单调递减,所以当x=0时,函数y=取最大值,且最大值为=1.故选C.
第1步:确定A(x)的图象和f'(x)的图象
若虚线是函数f(x)的图象,实线是函数f'(x)的图象,则函数f(x)有增有减,则f'(x)有正有负,与题图不符,所以实线是函数∮(x)的图象,虚线是函数f'(x)的图象.由题图可知∮
(0)=
1∮'
(0)=1,f,(x)≥0恒成立,所以函数f(x)在R上单调递增,且∮(x)≥0恒成立.(题眼)
第2步:研究函数y=f(x).e;的最值
因为y=∮(x).e²,所以y'=e²(A(x)+f−(x))≥0恒成立,所以函数y=f(x).e在R上单调递增,所以函数y=f(x).e²无最值第3步:研究函数y=八的最值
因为y=,所以y、=∠(x)|f(x)当x>0时,由题图可知∮(x)>f'(x),所以y'<0;当x<0时,由题图可知,f'(x)>f(x),所以y,>0.所以函数y=在(−∞,,0)上单调递增,在(0',+∞))上单调递减,所以当x=0时,函数y=取最大值,且最大值为=1.故选C.
9.已知$f(x)=A\sin(\omega x + \varphi)(A>0,\omega>0,0<\varphi<\frac{\pi}{2})$的部分图象如图所示,则

A.$f(0)=1$
B.$f(x)$在区间$(\frac{4\pi}{3},\frac{11\pi}{6})$上单调递减
C.$f(x)$在区间$[\frac{\pi}{3},\frac{5\pi}{6}]$上的值域为$[-1,\sqrt{3}]$
D.$f(x)$在区间$(\frac{\pi}{2},2\pi)$上有3个极值点

A.$f(0)=1$
B.$f(x)$在区间$(\frac{4\pi}{3},\frac{11\pi}{6})$上单调递减
C.$f(x)$在区间$[\frac{\pi}{3},\frac{5\pi}{6}]$上的值域为$[-1,\sqrt{3}]$
D.$f(x)$在区间$(\frac{\pi}{2},2\pi)$上有3个极值点
答案:
9.AD 三角函数的图象与性质+极值点设T为函数f(x)的最小正周期,由题图可知$\frac{3}{4}$T=$\frac{11π}{12}$−$\frac{H}{6}$=$\frac{3}{4}$,所以T=π,即2=ππ,所以∞=2.又由题图可知A=2,所以f(x)=2sin(2x+),因为函数∮(x)的图象过点($\frac{H}{6}$,2),所以sin(2×$\frac{H}{6}$+p)=1,即$\frac{H}{3}$+p=$\frac{T}{2}$+2kπ(k∈Z),则=$\frac{T}{6}$+2kπ(k∈Z),因为0<<$\frac{T}{2}$,所以=$\frac{T}{6}$,即f(x)=2sin(2x+$\frac{H}{6}$).(题眼)
对于Af
(0)=2sin$\frac{H}{6}$=1,所以选项A正确;
对于B,当x∈($\frac{4π}{3}$,$\frac{11π}{6}$)时,t=2x+$\frac{H}{6}$∈($\frac{17π}{6}$,$\frac{23}{6}$),因为函数y=sint在区间($\frac{17π}{6}$,$\frac{23}{6}$)上不单调,所以函数f(x)=
2sin(2x+$\frac{H}{6}$)在区间($\frac{4π}{3}$,$\frac{11π}{6}$)上不单调,所以选项B错误;对于C,当x∈[$\frac{T}{3}$,$\frac{5π}{6}$]时,t=2x+$\frac{H}{6}$∈[$\frac{5π}{6}$$\frac{11π}{6}$],所以sint∈
[−1,$\frac{1}{2}$],则函数∮(x)=2sin(2x+$\frac{T}{6}$)在区间[$\frac{H}{3}$,$\frac{5π}{6}$]上的值域为[−2,1],所以选项C错误;
对于D,当x∈($\frac{H}{2}$,2π)时,t=2x+$\frac{T}{6}$E($\frac{7π}{6}$,$\frac{25π}{6}$),由函数y=
sint的图象可知,y=sint在区间($\frac{7π}{6}$$\frac{25}{6}$π)上有3个极值点,所以函数f(x)=2sin(2x+$\frac{T}{6}$)在区间($\frac{H}{2}$,2π)上有3个极值点,所以选项D正确,综上,选AD.
对于Af
(0)=2sin$\frac{H}{6}$=1,所以选项A正确;
对于B,当x∈($\frac{4π}{3}$,$\frac{11π}{6}$)时,t=2x+$\frac{H}{6}$∈($\frac{17π}{6}$,$\frac{23}{6}$),因为函数y=sint在区间($\frac{17π}{6}$,$\frac{23}{6}$)上不单调,所以函数f(x)=
2sin(2x+$\frac{H}{6}$)在区间($\frac{4π}{3}$,$\frac{11π}{6}$)上不单调,所以选项B错误;对于C,当x∈[$\frac{T}{3}$,$\frac{5π}{6}$]时,t=2x+$\frac{H}{6}$∈[$\frac{5π}{6}$$\frac{11π}{6}$],所以sint∈
[−1,$\frac{1}{2}$],则函数∮(x)=2sin(2x+$\frac{T}{6}$)在区间[$\frac{H}{3}$,$\frac{5π}{6}$]上的值域为[−2,1],所以选项C错误;
对于D,当x∈($\frac{H}{2}$,2π)时,t=2x+$\frac{T}{6}$E($\frac{7π}{6}$,$\frac{25π}{6}$),由函数y=
sint的图象可知,y=sint在区间($\frac{7π}{6}$$\frac{25}{6}$π)上有3个极值点,所以函数f(x)=2sin(2x+$\frac{T}{6}$)在区间($\frac{H}{2}$,2π)上有3个极值点,所以选项D正确,综上,选AD.
查看更多完整答案,请扫码查看


