2025年一遍过八年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一遍过八年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
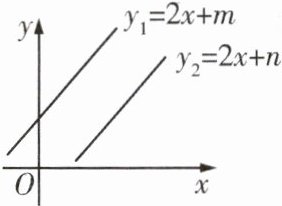
8[2023邯郸育华实验学校月考]已知一次函数y1=2x+m与y2=2x+n(m≠n)的图像如图所示,则关于x与y的二元一次方程组 的解有(
的解有(
A.0个
B.1个
C.2个
D.无数个
 的解有(
的解有( 
A.0个
B.1个
C.2个
D.无数个
答案:
A
∵一次函数y1=2x+m与y2=2x+n(m≠n)的图像是两条互相平行的直线,
∴关于x与y的二元一次方程组{22xx−−yy==−−mn,无解.
∵一次函数y1=2x+m与y2=2x+n(m≠n)的图像是两条互相平行的直线,
∴关于x与y的二元一次方程组{22xx−−yy==−−mn,无解.
9[2024呼伦贝尔中考]点P(x,y)在直线y= +4上,坐标(x,y)是二元一次方程5x−6y=33的解,则点P的位置在 (
+4上,坐标(x,y)是二元一次方程5x−6y=33的解,则点P的位置在 (
A.第一象限 B.第二象限
C.第三象限 D.第四象限
 +4上,坐标(x,y)是二元一次方程5x−6y=33的解,则点P的位置在 (
+4上,坐标(x,y)是二元一次方程5x−6y=33的解,则点P的位置在 ( A.第一象限 B.第二象限
C.第三象限 D.第四象限
答案:
D 联立方程,得{y=−$\frac{3}{4}$x+4'解得{xy==6−,$\frac{1}{2}$,
∴点P
5x−6y=33,
的坐标为(6,−$\frac{1}{2}$),
∴点P在第四象限
∴点P
5x−6y=33,
的坐标为(6,−$\frac{1}{2}$),
∴点P在第四象限
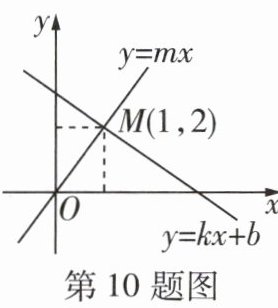
10[2024邯郸汉光中学期末]如图所示,一次函数y=kx+b(k,b是常数,k≠0)与正比例函数y=mx(m是常数,m≠0)的图像相交于点M(1,2),下列判断错误的是 ( )
A.关于x的方程mx=kx+b的解是x=1
B.关于x的不等式mx<kx+b的解集是x>1
C.当x<0时,函数y=kx+b的值比函数y=
mx的值大
D.关于x,y的方程组 ”的解是
”的解是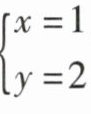

A.关于x的方程mx=kx+b的解是x=1
B.关于x的不等式mx<kx+b的解集是x>1
C.当x<0时,函数y=kx+b的值比函数y=
mx的值大
D.关于x,y的方程组
 ”的解是
”的解是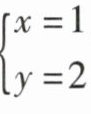
答案:
B
∵一次函数y=kx+b(k,b是常数,k≠0)与正比例函数y=mx(m是常数,m≠0)的图像相交于点M(1,2),
∴关于x的方程mx=kx+b的解是x=1,关于x,y的方程组{yy−−mkxx==b0,,的解是{xy==21,,故A,D正确;关于x的不等式mx<kx+b的解集是x<1,故B错误;当x<0时,函数y=
kx+b的图像在函数y=mx的图像的上面,
∴函数y=kx+b 的值比函数y=mx的值大,故C正确.
∵一次函数y=kx+b(k,b是常数,k≠0)与正比例函数y=mx(m是常数,m≠0)的图像相交于点M(1,2),
∴关于x的方程mx=kx+b的解是x=1,关于x,y的方程组{yy−−mkxx==b0,,的解是{xy==21,,故A,D正确;关于x的不等式mx<kx+b的解集是x<1,故B错误;当x<0时,函数y=
kx+b的图像在函数y=mx的图像的上面,
∴函数y=kx+b 的值比函数y=mx的值大,故C正确.
变式如图,直线y=kx(k≠0)与y=$\frac{2}{3}$x+2 在第二象限内交于点A,直线y=x2 +2分别交x轴、y轴于点B,C,3S△ABo=S△BOc,则方程组 的解为 (
的解为 (

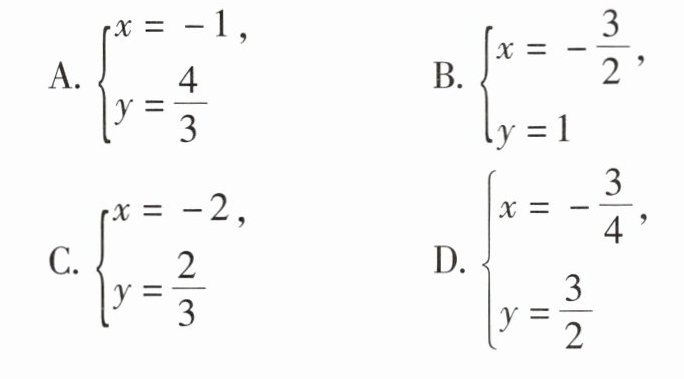
 的解为 (
的解为 ( 
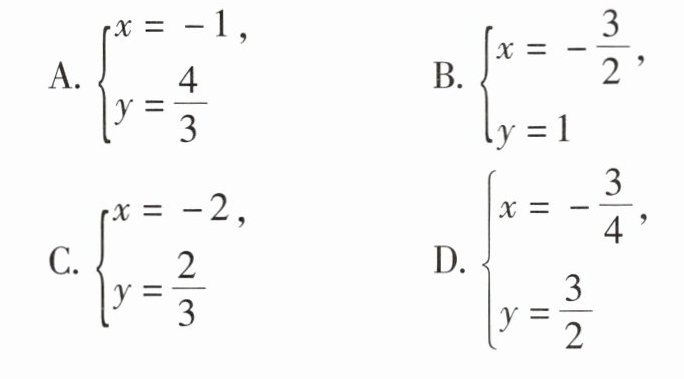
答案:
C 由y=$\frac{2}{3}$x+2可得,B(−3,0),C(0,2).
∴BO=3,0C=2,设点A的纵坐标为yA
∵3S△ABO=S△BOC,
∴3×$\frac{1}{2}$x
3×1y1=$\frac{1}{2}$x3x2,解得yA=±$\frac{2}{3}$.又
∵点A在第二象限内,
∴yA=$\frac{2}{3}$.当y=$\frac{2}{3}$时,$\frac{2}{3}$=$\frac{2}{3}$x+2,解得x=−2,
∴易知方程组kx−y=0, 的解为x=−2,
{2x−3y=−6 {y=$\frac{2}{3}$.
∴BO=3,0C=2,设点A的纵坐标为yA
∵3S△ABO=S△BOC,
∴3×$\frac{1}{2}$x
3×1y1=$\frac{1}{2}$x3x2,解得yA=±$\frac{2}{3}$.又
∵点A在第二象限内,
∴yA=$\frac{2}{3}$.当y=$\frac{2}{3}$时,$\frac{2}{3}$=$\frac{2}{3}$x+2,解得x=−2,
∴易知方程组kx−y=0, 的解为x=−2,
{2x−3y=−6 {y=$\frac{2}{3}$.
11嘉嘉在解方程组 ,的过程中,错把b 看成了6,其余的解题过程没有出错,解得此方程组的解为
,的过程中,错把b 看成了6,其余的解题过程没有出错,解得此方程组的解为 ,已知直线y=kx+b过点(3,−1),则b的正确值是__________.
,已知直线y=kx+b过点(3,−1),则b的正确值是__________.
 ,的过程中,错把b 看成了6,其余的解题过程没有出错,解得此方程组的解为
,的过程中,错把b 看成了6,其余的解题过程没有出错,解得此方程组的解为 ,已知直线y=kx+b过点(3,−1),则b的正确值是__________.
,已知直线y=kx+b过点(3,−1),则b的正确值是__________.
答案:
−13 将{xy==2−1,和b=6代入y=kx+b,得2=−k+
6,解得k=4.把(3,−1)代入y=4x+b中,得−1=3x4+b,
∴b=−13.
6,解得k=4.把(3,−1)代入y=4x+b中,得−1=3x4+b,
∴b=−13.
12−题多解如图,一次函数y=kx+b的图像经过点A(0,3),B(4,−3),则关于x的不等式kx+b+3<0的解集为________.
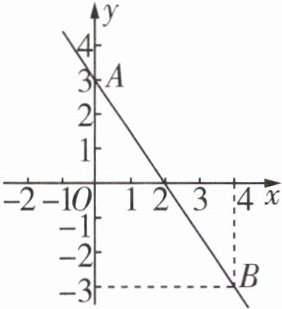

答案:
x>4 解法−
∵一次函数y=kx+b的图像经过点
B(4,−3),
∴当x=4时,kx+b=−3,由题图易知,y随x的增大而减小,
∴当x>4时,kx+b<−3,
∴关于x的不等式kx+b+3<0的解集是x>4.
解法二 把(0,3),(4,−3)分别代入y=kx+b,得{4bk=+3b,=−3,解得{k=−$\frac{3}{2}$,
∴一次函数的表达式为
b=3,
y=−x3 +3,
∴−x3 +3+3<0,解得x>4.
解法三 不等式可化为kx+b<−3,数形结合知,当x>4时,直线y=kx+b在直线y=−3的下方,故所求的解集为x>4.
∵一次函数y=kx+b的图像经过点
B(4,−3),
∴当x=4时,kx+b=−3,由题图易知,y随x的增大而减小,
∴当x>4时,kx+b<−3,
∴关于x的不等式kx+b+3<0的解集是x>4.
解法二 把(0,3),(4,−3)分别代入y=kx+b,得{4bk=+3b,=−3,解得{k=−$\frac{3}{2}$,
∴一次函数的表达式为
b=3,
y=−x3 +3,
∴−x3 +3+3<0,解得x>4.
解法三 不等式可化为kx+b<−3,数形结合知,当x>4时,直线y=kx+b在直线y=−3的下方,故所求的解集为x>4.
13教材P108B组T2变式[2023石家庄裕华区期末]如图,函数y=2x−2的图像与y轴交于点A,函数y2=−2x+6的图像与y轴交于点
B,两者相交于点C.
(1)方程组 的解是________.
的解是________.
(2)当y1>0与y2>0同时成立时,x的取值范围为________.
(3)求△ABC的面积.
(4)在函数y1=2x−2的图像上存在异于点C 的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
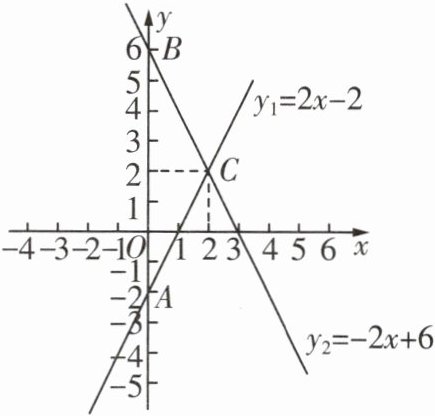
B,两者相交于点C.
(1)方程组
 的解是________.
的解是________.(2)当y1>0与y2>0同时成立时,x的取值范围为________.
(3)求△ABC的面积.
(4)在函数y1=2x−2的图像上存在异于点C 的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.

答案:
解:
(1) ,
,
(2)1<x<3
(3)由题图可知,点A,B的坐标分别为(0,−2),(0,6),
所以AB=8,所以SAβC=$\frac{1}{2}$x8×2=8.
(4)令点P(xo,2x−2),
则SAβP=$\frac{1}{2}$x8×1x1=8,所以x=±2.
−2,−6).
解:
(1)
 ,
,(2)1<x<3
(3)由题图可知,点A,B的坐标分别为(0,−2),(0,6),
所以AB=8,所以SAβC=$\frac{1}{2}$x8×2=8.
(4)令点P(xo,2x−2),
则SAβP=$\frac{1}{2}$x8×1x1=8,所以x=±2.
−2,−6).
查看更多完整答案,请扫码查看


