《2025年一遍过八年级数学下册冀教版》

1. 刹车距离是指车辆在行驶过程中从开始刹车到车辆完全停止所行驶的距离，主要取决于车速、摩擦系数、车重、路面状况等因素. 为了测定某种型号新能源汽车的刹车性能(车速不超过 120 km/h )，对这种型号的新能源汽车进行了测试，测得的数据如下表：

【基础设问】
(1)在这个变化过程中，自变量是________，因变量是________.
(2)观察表格，找出规律：刹车时车速每增加10 km/h，刹车距离增加________m，据此补全表格.
(3)在不超速的情况下，最大的刹车距离为________m.
(4)请用关系式表示变量$s$与$v$之间的数量关系.
【能力设问】
(5)当刹车距离为 18 m 时，求刹车时的车速.
(6)若该型号新能源汽车以 90 km/h 的速度前行，且与前车保持直线距离 20 m，若遭遇紧急情况，司机紧急制动后是否会发生追尾事故？

答案：
解：\n
(1) 刹车时车速 刹车距离\n
(2) 2.4
补全表格如下：

在不超速的情况下，最大车速为 120 km/h，此时的刹车距离为 $12×2.4 = 28.8(m)$。\n
(4)
∵ 当刹车时车速每增加 10 km/h 时，刹车距离增加 2.4 m，
$\therefore s = 2.4×\frac{v}{10}=0.24v$，
$\therefore$ 变量 $s$ 与 $v$ 之间的数量关系为 $s = 0.24v$。\n
(5) 将 $s = 18$ 代入 $s = 0.24v$ 中，得 $18 = 0.24v$，
解得 $v = 75$，
$\therefore$ 当刹车距离为 18 m 时，刹车时的车速为 75 km/h。\n
(6) 当 $v = 90$ 时，$s = 0.24×90 = 21.6＞20$，
$\therefore$ 司机紧急制动后会发生追尾事故。

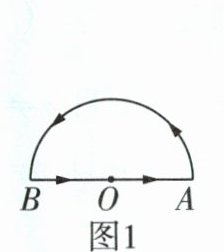
2. 嘉淇在一个半圆形的花园的周边散步，如图1，嘉淇从圆心$O$出发，按图中箭头所示的方向，依次匀速走完下列三条线路：(1)线段$OA$；(2)半圆弧$AB$；(3)线段$BO$，回到出发点. 嘉淇离出发点的距离$s$(嘉淇所在位置与$O$点之间线段的长度)与时间$t$之间的图像如图2所示，请回答下列问题(圆周率$\pi$的值取 3 )：

【基础设问】
(1)花园的半径是________米，嘉淇的速度是________米/分.
(2)写出$0\leq t\leq2$时$s$与$t$之间的关系式，指出其中的自变量、因变量和常量.
(3)$a$分时，嘉淇位于花园的哪个位置？求$a$的值.
【能力设问】
(4)若沿途只有一处嘉淇遇到了一位同学，停下来交谈了 2 分钟，并且嘉淇在遇到同学的前后，始终保持速度不变，请你求出：
①嘉淇遇到同学的地方离出发点的距离；
②嘉淇返回到起点$O$经历的时间.

答案： 解：\n
(1) 100 50
由图像，可知花园的半径为 100 米，嘉淇的速度为 $100÷2 = 50$（米/分）。\n
(2) 当 $0\leq t\leq2$ 时，$s$ 与 $t$ 之间的关系式为 $s = 50t$，
其中 $t$ 是自变量，$s$ 是因变量，50 是常量。\n
(3) 结合题图，可知 2 分到 $a$ 分期间，嘉淇位于半圆弧 $AB$ 上，
$\therefore a$ 分时，嘉淇位于点 $B$ 的位置。
$\because$ 半圆弧长为 $100\pi = 300$ 米，
$\therefore a = 2+\frac{300}{50}=8$（分）。\n
(4) ① 易知嘉淇在 $t = 9$ 时遇到同学，路程为 450 米，
$\because$ 全程长 $100 + 300+100 = 500$（米），$\therefore$ 嘉淇离出发点距离为 50 米。
② 嘉淇返回到起点 $O$ 经历的时间为 $\frac{500}{50}+2 = 12$（分）。