《2025年一遍过八年级数学下册冀教版》

6 [2024承德二中月考]某校七年级四个班的男、女生人数如图所示. 根据图中提供的信息，下列四种说法中正确的是（ ）

A. 七（2）班学生最少
B. 七（3）班男生是女生的2倍
C. 七（4）班女生比男生多
D. 七（2）班和七（4）班学生一样多

答案： B 从题图中可知七
(1)班男生、女生的人数都是最少的，所以七
(1)班学生最少，故A错误；七
(3)班女生10人，男生20人，所以七
(3)班男生是女生的2倍，故B正确；七
(4)班女生比男生少，故C错误；七
(2)班和七
(4)班女生一样多，但七
(4)班男生较多，所以七
(4)班学生较多，故D错误。

7 某公司生产的一种产品按照质量由高到低分为A，B，C，D四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍. 为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：

根据以上信息，下列推断合理的是（ ）
A. 改进生产工艺后，A级产品的数量没有变化
B. 改进生产工艺后，D级产品的数量减少
C. 改进生产工艺后，C级产品的数量减少
D. 改进生产工艺后，B级产品的数量增加了不到一倍

答案： C 设原生产总量为1，则改进后生产总量为2，所以原A，B，C，D等级的生产量分别为0.3，0.37，0.28，0.05，改进后四个等级的生产量分别为0.6，1.2，0.12，0.08，所以改进生产工艺后，A级产品的数量增加，D级产品的数量增加，C级产品的数量减少，B级产品的数量增加了超过一倍。

8 [2024沧州检测]某校学生会主席竞选中，参与投票的学生必须从进入决赛的4名选手(A，B，C，D)中选1名，且只能选1名进行投票，根据投票结果，绘制了如图所示的两幅不完整的统计图，条形统计图(柱的高度从高到低排列)被墨迹遮盖了一部分，针对未标明的统计数据，三人的说法如下：
甲：条形统计图中“( )”应填的选手是A；
乙：n的值为30；丙：选手B的票数是120票.
下列判断正确的是（ ）


A. 乙错，丙对
B. 甲和乙都错
C. 乙对，丙错
D. 甲错，丙对

答案： C 参与投票的学生有$40\div10\% = 400$(人)，由题图可知A所占的百分比最多，
∴选手A的票数最多，故条形统计图中“( )”内应填的选手是A.
∵扇形统计图中扇形B所对应的圆心角的度数是$90^{\circ}$，
∴该扇形所占整圆的比例为25%，
∴$n\% = 1 - 10\% - 35\% - 25\% = 30\%$，选手B的票数为$400\times25\% = 100$(票)，
∴$n = 30$，故甲和乙对，丙错。

9 [2023青岛三十七中期末]某学校将为七年级学生开设A，B，C，D，E，F共6门选修课，随机选取若干名学生进行了“我最喜欢的一门选修课”的调查，将调查结果绘制成如下尚不完整的统计图表. 根据图表提供的信息，下列结论错误的是（ ）

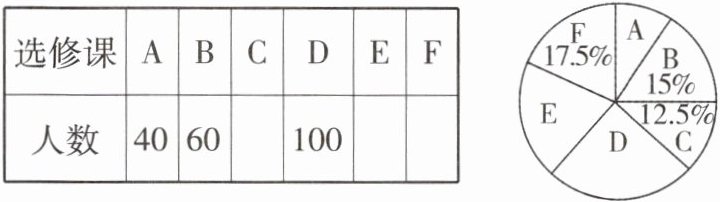
A. 这次被调查的学生人数为400
B. 被调查的学生中最喜欢选修课E，F的人数分别为80，70
C. 最喜欢选修课C的人数最少
D. 扇形统计图中E部分扇形的圆心角度数为72°

答案： C 由题意可知，被调查的学生人数为$60\div15\% = 400$，所以选项A结论正确；因为$\frac{100}{400}\times360^{\circ} = 90^{\circ}$，$\frac{40}{400}\times360^{\circ} = 36^{\circ}$，$360^{\circ}\times(17.5\% + 15\% + 12.5\%) = 162^{\circ}$，所以扇形统计图中E部分扇形的圆心角度数为$360^{\circ} - 162^{\circ} - 90^{\circ} - 36^{\circ} = 72^{\circ}$，所以选项D结论正确；因为$400\times\frac{72^{\circ}}{360^{\circ}} = 80$，$400\times17.5\% = 70$，所以本次被调查的学生中最喜欢选修课E，F的人数分别为80，70，所以选项B结论正确；因为$\frac{40}{400}\times100\% = 10\%$，$12.5\%＞10\%$，所以最喜欢选修课A的人数最少，所以选项C结论错误。

10 [新考法] [2024邢台十九中月考]小明对本校八年级530名学生的体育达标情况进行调查，按A，B，C三等成绩进行统计并制作出如图所示的统计图，其中(1)班有50人，A等级成绩为达标以上，B等级成绩为达标，C等级成绩为不达标，根据图中信息解答下面问题：

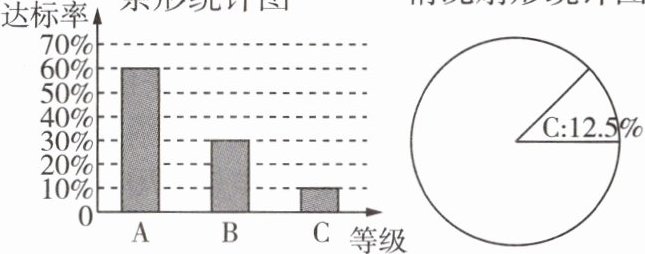
(1)若除(1)班外，其他班级学生体育考试成绩在B等级的有120人.
①分别计算其余班级体育考试成绩A等级、B等级所对应的扇形的圆心角度数；
②请补全扇形统计图.
(2)若要求全年级学生的体育达标率(包括达标和达标以上)不低于90%，在本次调查中，该年级全体学生的体育达标率是否符合要求？如果不符合要求，至少还需要使几个不达标同学的成绩变为达标(或以上)？

答案：
解：
(1)其余各班的人数为$530 - 50 = 480$，
B等级成绩的人数所占的百分比为$\frac{120}{480}\times100\% = 25\%$，所对应扇形圆心角的度数为$360^{\circ}\times25\% = 90^{\circ}$，
A等级成绩的人数所占的百分比为$1 - 25\% - 12.5\% = 62.5\%$，所对应扇形圆心角的度数为$360^{\circ}\times62.5\% = 225^{\circ}$。
补全扇形统计图如下：

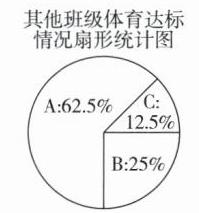
(2)该年级全体学生的体育达标率不符合要求。根据条形统计图，得
(1)班学生体育达标率为$0.6 + 0.3 = 0.9 = 90\%$，达标人数为$50\times0.9 = 45$(人)；
根据扇形统计图，得本年级其余各班学生体育达标率为$1 - 12.5\% = 87.5\%$，达标人数为$480\times0.875 = 420$(人)，
∴全年级学生的体育达标率为$\frac{45 + 420}{530}\times100\%\approx87.7\%＜90\%$，
∴该年级全体学生的体育达标率不符合要求。
设需要增加x个同学的成绩达标，$\frac{x + 45 + 420}{530}\geq90\%$，解得$x\geq12$。
答：至少还需要使12个不达标同学的成绩变为达标。