2025年一遍过八年级数学下册冀教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年一遍过八年级数学下册冀教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
1 [教材P67练习T1变式][2024唐山二十六中月考]函数$y = \frac{2}{3 - x}$中自变量$x$的取值范围是( )
A. $x > 3$
B. $x < 3$
C. $x \neq 3$
D. $x \neq - 3$
A. $x > 3$
B. $x < 3$
C. $x \neq 3$
D. $x \neq - 3$
答案:
C 根据分式有意义的条件,得3 - x≠0,得x≠3.
2 [2023保定期末]函数$y = \sqrt{3x - 1} - 2$中自变量$x$的取值范围是( )
A. $x \geq \frac{1}{3}$
B. $x \geq 2$
C. $x \leq \frac{1}{3}$
D. $x \neq \frac{1}{3}$
A. $x \geq \frac{1}{3}$
B. $x \geq 2$
C. $x \leq \frac{1}{3}$
D. $x \neq \frac{1}{3}$
答案:
A
3 如图,数轴上表示的是某个函数表达式的自变量$x$的取值范围,则这个函数表达式可以是( )
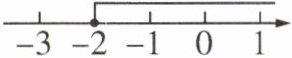
A. $y = x + 2$
B. $y = x^{2} + 2$
C. $y = \frac{1}{\sqrt{x + 2}}$
D. $y = \sqrt{x + 2}$
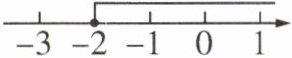
A. $y = x + 2$
B. $y = x^{2} + 2$
C. $y = \frac{1}{\sqrt{x + 2}}$
D. $y = \sqrt{x + 2}$
答案:
D 分析如下:

D 分析如下:

4 函数$y = \frac{\sqrt{x + 3}}{x^{2} - 1} + (x + 3)^{0}$中自变量$x$的取值范围是____________.
答案:
x > -3且x≠±1 由题意,得x² - 1≠0且x + 3≥0且x + 3≠0,解得x > -3且x≠±1.
5 [2024兰州五十三中期中]一长为5 m,宽为2 m的长方形木板,现在在长边上截去长为$x$ m的一部分(如图),则剩余木板的面积$y$ m²与$x$ m的关系式为( )

A. $y = 2x(x \geq 0)$
B. $y = 5x(0 \leq x < 5)$
C. $y = 10 - 2x(0 \leq x < 5)$
D. $y = 10 - 2x(x \geq 0)$

A. $y = 2x(x \geq 0)$
B. $y = 5x(0 \leq x < 5)$
C. $y = 10 - 2x(0 \leq x < 5)$
D. $y = 10 - 2x(x \geq 0)$
答案:
C 依题意,得y = 2×5 - 2x = 10 - 2x,0≤x < 5.
6 [教材P68练习T2变式]已知A,B两地相距3千米,小黄从A地到B地,平均速度为4千米/时,若用$x$(时)表示行走的时间,$y$(千米)表示余下的路程,则$y$关于$x$的函数表达式是( )
A. $y = 4x(x \geq 0)$
B. $y = 4x - 3(x \geq \frac{3}{4})$
C. $y = 3 - 4x(x \geq 0)$
D. $y = 3 - 4x(0 \leq x \leq \frac{3}{4})$
A. $y = 4x(x \geq 0)$
B. $y = 4x - 3(x \geq \frac{3}{4})$
C. $y = 3 - 4x(x \geq 0)$
D. $y = 3 - 4x(0 \leq x \leq \frac{3}{4})$
答案:
D 根据题意,得走完全程需要的时间为3÷4 = $\frac{3}{4}$(时),所以y关于x的函数表达式是y = 3 - 4x(0≤x≤$\frac{3}{4}$).
7 已知某银行的存款月利率为0.225%,现存款1 000元,则本息和$y$(元)与存期$x$(月)之间的函数关系式为____________,自变量的取值范围是____________.
答案:
y = 1 000 + 2.25x x≥0且x为整数(或x为自然数)
8 用长为12米的竹篱笆围成一个如图所示的长方形养鸡场(篱笆用完),养鸡场的一边靠墙,另三边用竹篱笆围成.设养鸡场与墙壁垂直的一边长为$x$米,与墙壁平行的一边长为$y$米.
(1)写出$y$与$x$之间的函数关系式;
(2)不考虑墙壁的长度,求自变量$x$的取值范围;
(3)如果墙壁的长为5米,其他条件不变,求自变量$x$的取值范围.

(1)写出$y$与$x$之间的函数关系式;
(2)不考虑墙壁的长度,求自变量$x$的取值范围;
(3)如果墙壁的长为5米,其他条件不变,求自变量$x$的取值范围.

答案:
解:
(1)由题意,得y + 2x = 12,所以y与x之间的函数关系式为y = -2x + 12.
(2)易知 -2x + 12 > 0且x > 0,所以0 < x < 6,即自变量x的取值范围是0 < x < 6.
(3)由
(2)可知0 < x < 6.因为墙壁的长为5米,所以y≤5,即12 - 2x≤5,所以3.5≤x < 6.
(1)由题意,得y + 2x = 12,所以y与x之间的函数关系式为y = -2x + 12.
(2)易知 -2x + 12 > 0且x > 0,所以0 < x < 6,即自变量x的取值范围是0 < x < 6.
(3)由
(2)可知0 < x < 6.因为墙壁的长为5米,所以y≤5,即12 - 2x≤5,所以3.5≤x < 6.
查看更多完整答案,请扫码查看


