《2025年一遍过八年级数学下册冀教版》

1 [2024通辽中考]如图，在同一平面直角坐标系中，一次函数$y = k_1x + b_1$与$y = k_2x + b_2$（其中$k_1k_2\neq0,k_1,k_2,b_1,b_2$为常数）的图像分别为直线$l_1,l_2$. 下列结论正确的是 （ ）

A. $b_1 + b_2 ＞ 0$
B. $b_1b_2 ＞ 0$
C. $k_1 + k_2 ＜ 0$
D. $k_1k_2 ＜ 0$

答案： A　由−次函数$l_1:y = k_1x + b_1$的图像可得$k_1＞0,b_1＞1$,由一次函数$l_2:y = k_2x + b_2$的图像可得$k_2＞0,b_2 = -1$,
∴$b_1 + b_2＞0,b_1b_2＜0,k_1 + k_2＞0,k_1k_2＞0$,故A项中的结论正确.

2 [2024西安交大附中模拟]若点$(m,n)$在第二象限，则函数$y = -nx + m - n$的图像可能是 （ ）

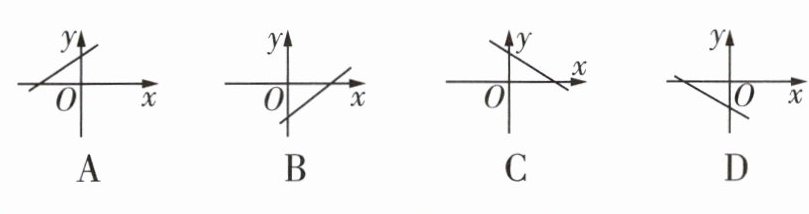
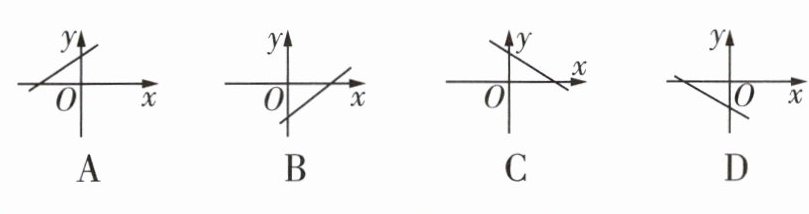
答案： D
∵点$(m,n)$在第二象限,
∴$m＜0,n＞0$,
∴$ - n＜0,m - n＜0$,
∴函数$y = -nx + m - n$的图像经过第二、三、四象限.

3 [2023秦皇岛期末]若一次函数$y = kx + b$的图像如图所示，则函数$y = - 3kx - b$的图像可能为 （ ）

答案： B　由题图知,一次函数$y = kx + b$的图像经过第一、二、四象限,所以$k＜0,b＞0$,所以$ - 3k＞0, - b＜0$,所以函数$y = -3kx - b$的图像经过第一、三、四象限，且倾斜度大.

4 [2024石家庄期中]已知点$A(x_1,y_1),B(x_2,y_2)$在直线$y = kx + b(k\neq0)$上，当$x_1 ＜ x_2$时，$y_1 ＜ y_2$，且$kb ＞ 0$，则在平面直角坐标系中，它的图像大致是 （ ）

答案： A
∵点$A(x_1,y_1),B(x_2,y_2)$在直线$y = kx + b(k\neq0)$上,当$x_1＜x_2$时,$y_1＜y_2$,
∴$k＞0$.又
∵$kb＞0$,
∴$b＞0$,
∴直线$y = kx + b$经过第一、二、三象限.

5 一次函数$y = mx + n$与正比例函数$y = mnx(m,n$是常数，且$mn\neq0)$在同一平面直角坐标系中的图像可能是 （ ）

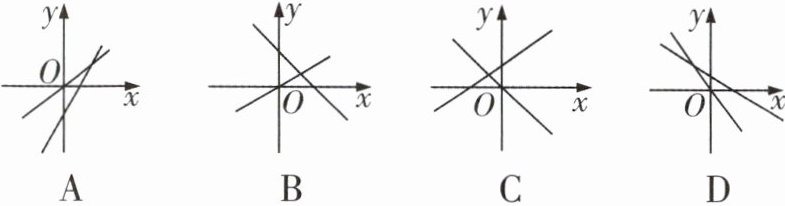
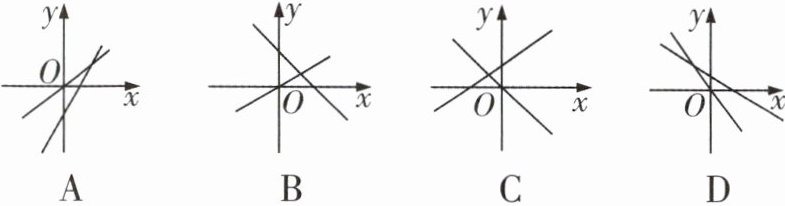
答案： D　A项,由一次函数的图像可知$m＞0,n＜0$,所以$mn＜0$,由正比例函数的图像可知$mn＞0$,所以A项错误;B项，由一次函数的图像可知$m＜0,n＞0$,所以$mn＜0$,由正比例函数的图像可知$mn＞0$,所以B项错误;C项，由一次函数的图像可知$m＞0,n＞0$,所以$mn＞0$,由正比例函数的图像可知$mn＜0$,所以C项错误;D项，由一次函数的图像可知$m＜0,n＞0$,所以$mn＜0$,由正比例函数的图像可知$mn＜0$,所以D项正确.

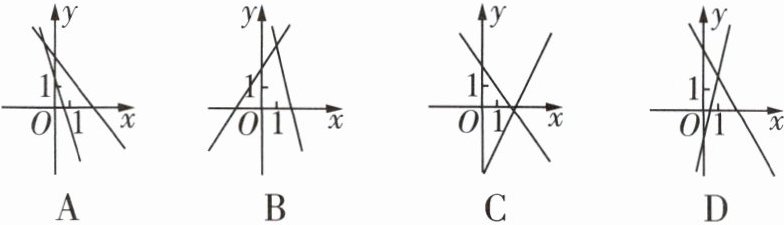
6 [一题多解[2022安徽中考]在同一平面直角坐标系中，一次函数$y = ax + a^2$与$y = a^2x + a$的图像可能是 （ ）

答案： D解法　当$x = 1$时,$y = ax + a²$与$y = a²x + a$的函数值都是$a² + a$,所以两直线交点的横坐标为$1$,排除选项A,C.
当$a＞0$时,$y = ax + a²$与$y = a²x + a$的图像都经过第一、二、三象限;当$a＜0$时,$y = ax + a²$的图像经过第一、二、四象限，$y = a²x + a$的图像经过第一、三、四象限.故选项D符合题意.
解法二　当$x = 1$时,$y = ax + a²$与$y = a²x + a$的函数值都是$a² + a$,所以两直线交点的横坐标为$1$,排除选项A,C.若$a＞0$,则$y = ax + a²$与$y = a²x + a$的图像都交在$x$轴的负半轴、$y$ 轴的正半轴;若$a＜0$,则$y = ax + a²$的图像交在$y$轴的正半轴,$y = a²x + a$的图像交在$y$轴的负半轴,所以选项D符合题意.