10. 某公司“咨询热线”电话共有8路外线,经长期统计发现,在8点到10点这段时间内,外线电话同时打入情况如下表所示:

(1)若这段时间内,公司只安排了2位接线员(一个接线员一次只能接一个电话)。
(I)求至少一种电话不能一次接通的概率;
(II)在一周五个工作日中,如果至少有三个工作日的这段时间(8点至10点)内至少一路电话不能一次接通,那么公司的形象将受到损害,现用该事件的概率表示公司形象的“损害度”,求上述情况下公司形象的“损害度”。
(2)求一周五个工作日的这段时间(8点至10点)内,电话同时打入数ξ的期望。
9. 一名学生每天骑车上学,从他家到学校的途中有6个交通岗,假设他在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 。
。
(1)设ξ为这名学生在途中遇到红灯的次数,求ξ的分布列;
(2)设η为这名学生在首次停车前经过的路口数,求η的分布列;
(3)求这名学生在途中至少遇到一次红灯的概率。
8. 有甲、乙两个盒子,甲盒子中有8张卡片,其中两张写有数字0,三张写有数字1,三张写有数字2;乙盒子中有8张卡片,其中三张写有数字0,两张写有数字1,三张写有数字2。
(1)如果从甲盒子中取两张卡片,从乙盒子中取一张卡片,那么取出的3张卡片都写有1的概率是多少?
(2)如果从甲、乙两个盒子中各取一张卡片,设取出的两张卡片数字之和为ξ,求ξ的分布列和期望值。
7. 袋子里有大小相同的3个红球和4个黑球,今从袋子里随机取出4个球。
(1)求取出的红球数ξ的概率分布列和数学期望;
(2)若取出每个红球得2分,取出每个黑球得1分,求得分不超过5分的概率。
6. 某种项目的射击比赛规则是:开始时在距目标100m处射击,如果命中记3分,同时停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m远处,这时命中记2分,同时停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m远处,若第三次命中则记1分,同时停止射击;若三次都未命中,则记0分,已知射手甲在100m处击中目标的概率为 ,他命中目标的概率与目标的距离的平方成反比,且各次射击都是独立的。
,他命中目标的概率与目标的距离的平方成反比,且各次射击都是独立的。
(1)求射手甲在200m处命中目标的概率;
(2)设射手甲得k分的概率为P0,求P3,P2,P1,P0的值;
(3)求射手甲在三次射击中击中目标的概率。

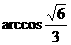 B.
B.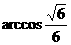 C.
C.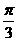 D.
D.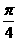
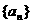 的公差为2,前
的公差为2,前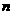 项和为
项和为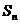 ,则下列结论中正确的是( )
,则下列结论中正确的是( )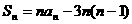 B.
B.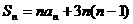
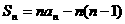 D.
D.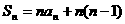
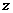 满足
满足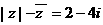 ,则
,则 的值是( )
的值是( )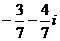 B.
B.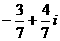 C.
C.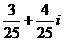 D.
D.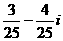
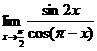 =( )
=( )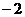 B.2
C.
B.2
C. D.1
D.1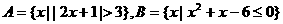 ,则
,则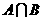 =( )
=( )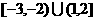 B.
B.
 D.
D.