6.O为平面上的定点,A、B、C是平面上不共线的三点,若( 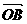 -
-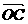 )·(
)·(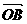 +
+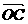 -2
-2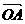 )=0,则DABC是( )
)=0,则DABC是( )
A.以AB为底边的等腰三角形 B.以BC为底边的等腰三角形
C.以AB为斜边的直角三角形 D.以BC为斜边的直角三角形
一项是符合题目要求的)
1.(文)函数 的定义域是 ( )
的定义域是 ( )
A.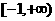 B.
B.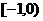 C.
C.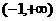 D.(-1,0)
D.(-1,0)
(理)复数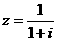 所对应的点在 ( )
所对应的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
20.解:(1)由于椭圆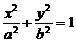 过点
过点 ,
,
故 . ………………………………………………………………………………………………………………1分
. ………………………………………………………………………………………………………………1分
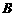 ,
, 横坐标适合方程
横坐标适合方程
解得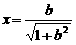 (
(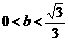 即
即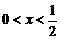 ).………………………………………………………4分
).………………………………………………………4分
即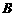 ,
, 横坐标是
横坐标是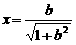 (
(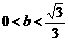 即
即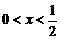 ).……………………………………5分
).……………………………………5分
(2)根据题意,可设抛物线方程为 . …………………6分
. …………………6分
∵ ,∴
,∴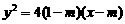 .………………………………………………………………7分
.………………………………………………………………7分
把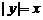 和
和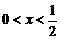 (等同于
(等同于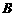 ,
, 坐标(
坐标(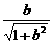 ,
,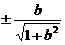 ))代入式抛物线方
))代入式抛物线方
程,得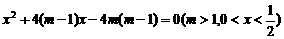 . ……………………………………9分
. ……………………………………9分
令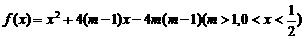 .……………………………………10分
.……………………………………10分
则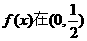 内有根(并且是单调递增函数),
内有根(并且是单调递增函数),
∴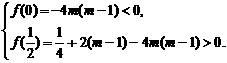 ………………………………………………………………13分
………………………………………………………………13分
解得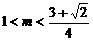 . …………………………………………………………………………………………14分
. …………………………………………………………………………………………14分
19.解:(1)根据题意,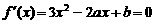 有解,
有解,
∴ 即
即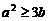 . ……………………………………………………………………………3分
. ……………………………………………………………………………3分
(2)若函数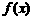 可以在
可以在 和
和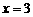 时取得极值,
时取得极值,
则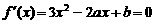 有两个解
有两个解 和
和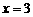 ,且满足
,且满足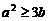 .
.
易得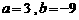 . ………………………………………………………………………………………………6分
. ………………………………………………………………………………………………6分
(3)由(2),得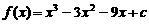 . ………………………………………………………………7分
. ………………………………………………………………7分
根据题意,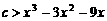 (
(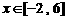 )恒成立. ……………………………………………9分
)恒成立. ……………………………………………9分
∵函数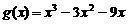 (
(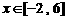 )在
)在 时有极大值
时有极大值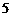 (用求导的方法),
(用求导的方法),
且在端点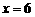 处的值为
处的值为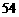 .
.
∴函数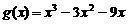 (
(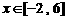 )的最大值为
)的最大值为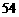 . …………………………13分
. …………………………13分
所以 . …………………………………………………………………………………………………………14分
. …………………………………………………………………………………………………………14分
18、(本题满分14分)
解:(1)设等差数列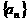 的公差为
的公差为 ,则
,则 …………… 2分
…………… 2分
∵
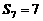 ,
,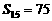 ,
,
∴ 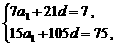 即
即
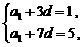 ……………
4分
……………
4分
解得
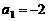 ,
,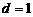 。……………………………………………… 6分
。……………………………………………… 6分
∴ 数列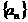 的通项公式为
的通项公式为 …………………… 7分
…………………… 7分
(2)  ………………………… 9分
………………………… 9分
∴ 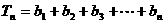

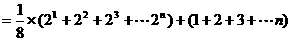
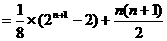

………………………… 14分
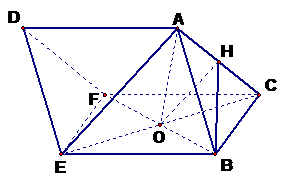
17、(Ⅰ) 证明:∵
证明:∵ 是菱形,
是菱形,
 ∴
∴ 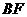 ⊥
⊥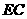 ……………………..1分
……………………..1分
又∵ 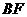 ⊥
⊥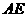 ,且
,且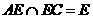
∴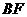 ⊥平面
⊥平面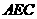 , ……………………..3分
, ……………………..3分
而AO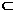 平面
平面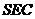
∴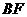 ⊥
⊥
∵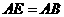 ,
, ∴
∴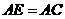
∴ ⊥
⊥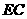 ,且
,且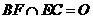
∴ ⊥平面
⊥平面 . ……………5分
. ……………5分
(Ⅱ) 取 的中点
的中点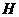 ,连结
,连结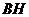 、
、
 ∵
∵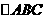 是等边三角形 ∴
是等边三角形 ∴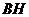 ⊥
⊥
∵ ⊥平面
⊥平面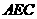 ∴
∴ 是
是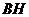 在平面
在平面 上的射影,∴由三垂线定理逆定理 可得
上的射影,∴由三垂线定理逆定理 可得
∴ 是二面角
是二面角 的平面角 ……………7分
的平面角 ……………7分
 ≌Rt
≌Rt ,则
,则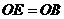 ,∴四边形
,∴四边形 为正方形。
为正方形。
在直角三角形 中,
中,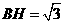 ,
,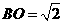 ∴
∴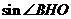 =
=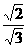 =
= ………9分
………9分
∴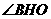 =arcsin
=arcsin .(或
.(或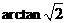 ,
,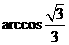 )
)
∴二面角 的大小是arcsin
的大小是arcsin …………………………………10分
…………………………………10分
(Ⅱ)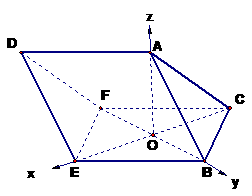 另解:由(Ⅰ)易证
另解:由(Ⅰ)易证 ≌Rt
≌Rt ,则
,则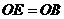 ,
,
∴四边形 为正方形。以
为正方形。以 为原点,
为原点,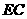 所在直线为
所在直线为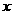 轴,
轴,
FB所在直线为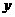 轴, OA所在直线为
轴, OA所在直线为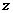 轴,建立空间直角坐标系(如图),则A(0,0,
轴,建立空间直角坐标系(如图),则A(0,0,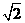 ), B(0,
), B(0, 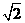 ,0),C(-
,0),C(-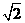 ,0,0),
,0,0),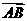 =(0,
=(0,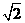 ,-
,-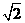 ),
),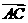 =(-
=(-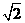 ,0,-
,0,-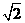 )
)
…………………………………………………………………….7分
设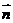 =(
=(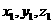 )为平面
)为平面 的法向量,则
的法向量,则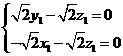
∴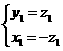 ,取
,取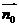 =(-1,1,1)为平面
=(-1,1,1)为平面 的一个法向量。……………8分
的一个法向量。……………8分
而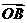 =(0,
=(0, 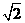 ,0)为平面
,0)为平面 的一个法向量。设
的一个法向量。设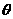 为
为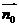 与
与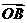 的夹角,则
的夹角,则 =
=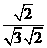 =
= ………………………………………………………….9分
………………………………………………………….9分
∴二面角 的大小为
的大小为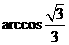 ……………………………………….10分
……………………………………….10分
(Ⅲ)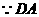 ∥
∥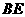 ,
,

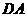 ∥平面
∥平面
∴点 、
、 到面
到面 的距离相等………………………………………………………11分
的距离相等………………………………………………………11分
 …………………………………………………………………..12分
…………………………………………………………………..12分
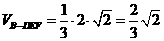 …………………………………………………………14分
…………………………………………………………14分

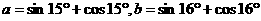 ,则下列各式中正确的是 ( )
,则下列各式中正确的是 ( )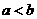 B.
B.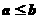 C.
C.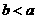 D.
D.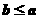
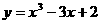 的单调减区间是( )
的单调减区间是( )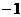 ,1) B.(1,2)
,1) B.(1,2) 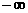 ,
, )
) 的通项公式为
的通项公式为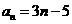 ,则
,则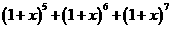 的展开式中含
的展开式中含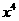 项的系数是该数列的 ( )
项的系数是该数列的 ( )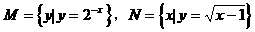 ,则
,则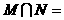 ( )
( )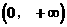 B.
B.
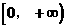
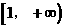 D.
D.

