22.解:设圆的圆心为P(a,b),半径为r,则P到x轴,y轴的距离分别为|b|、|a|,由题设知圆P截x轴所得劣弧所对圆心角为90°,故圆P截x轴所得弦长为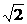 r=2b.
r=2b.
∴r2=2b2 ①又由y轴截圆得弦长为2,∴r2=a2+1 ②
由①、②知2b2-a2=1.又圆心到l:x-2y=0的距离d= ,∴5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1.当且仅当a=b时“=”号成立,
,∴5d2=(a-2b)2=a2+4b2-4ab≥a2+4b2-2(a2+b2)=2b2-a2=1.当且仅当a=b时“=”号成立,
∴当a=b时,d最小为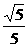 ,由
,由 得
得 或
或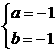 由①得r=
由①得r=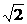 .
.
∴(x-1)2+(y-1)2=2或(x+1)2+(y+1)2=2为所求.
20.若动圆C与圆(x-2)2+y2=1外切,且和直线x+1=0相切.求动圆圆心C的轨迹E的方程.
解:设动圆的圆心C的坐标为(x,y),则x-(-1)+1=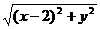 ,即x+2=
,即x+2=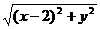 ,整理得y2=8x.所以所求轨迹E的方程为y2=8x.
,整理得y2=8x.所以所求轨迹E的方程为y2=8x.
21解:假设存在斜率为1的直线l,使l被圆C截得的弦AB为直径的圆过原点.设l的方程为y=x+b,A(x1,y1),B(x2,y2).
由OA⊥OB知,kOA·kOB=-1,即 =-1,∴y1y2=-x1x2.
=-1,∴y1y2=-x1x2.
由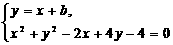 ,得2x2+2(b+1)x+b2+4b-4=0,
,得2x2+2(b+1)x+b2+4b-4=0,
∴x1+x2=-(b+1),x1·x2=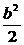 +2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
+2b-2,y1y2=(x1+b)(x2+b)=x1x2+b(x1+x2)+b2
=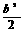 +2b-2-b(b+1)+b2=
+2b-2-b(b+1)+b2=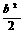 +b-2
+b-2
∵y1y2=-x1x2 ∴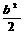 +b-2=-(
+b-2=-(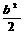 +2b-2) 即b2+3b-4=0.∴b=-4或b=1.
+2b-2) 即b2+3b-4=0.∴b=-4或b=1.
又Δ=4(b+1)2-8(b2+4b-4)=-4b2-24b+36=-4(b2+6b-9)
当b=-4时,Δ=-4×(16-24-9)>0; =1时,Δ=-4×(1+6-9)>0
故存在这样的直线l,它的方程是y=x-4或y=x+1,即x-y-4=0或x-y+1=0.
19.解:(1)圆x2+y2+8x-4y=0可写成(x+4)2+(y-2)2=20.
∵圆x2+y2+8x-4y=0与以原点为圆心的某圆关于直线y=kx+b对称,
∴y=kx+b为以两圆圆心为端点的线段的垂直平分线.∴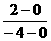 ×k=-1,k=2.
×k=-1,k=2.
点(0,0)与(-4,2)的中点为(-2,1),∴1=2×(-2)+b,b=5.∴k=2,b=5.
(2)圆心(-4,2)到2x-y+5=0的距离为d=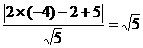 .
.
而圆的半径为2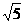 ,∴∠AOB=120°.
,∴∠AOB=120°.
18.解:(1)当两直线的斜率不存在时,方程分别为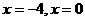 ,满足题意,
,满足题意,
当两直线的斜率存在时,设方程分别为 与
与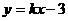 ,
,
即: 与
与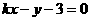 ,由题意:
,由题意: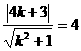 ,解得
,解得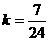 ,
,
所以,所求的直线方程分别为: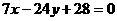 ,
, 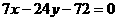
综上:所求的直线方程分别为: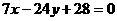 ,
,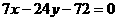 或
或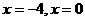 .
.
(2)由(1)当两直线的斜率存在时,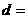
 ,∴
,∴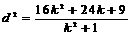 ,
,
∴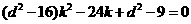 ,
,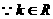 ∴
∴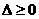 ,即
,即 ,
,
∴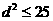 ,∴
,∴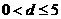 ,∴
,∴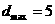 ,当
,当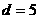 ,
,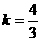 .
.
当两直线的斜率不存在时, , ∴
, ∴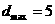 ,
,
此时两直线的方程分别为 ,
,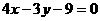 .
.

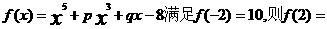
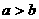 ”是“
”是“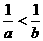 ”的
”的 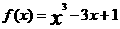 在闭区间[-3,0]上的最大值、最小值分别是
在闭区间[-3,0]上的最大值、最小值分别是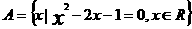 的所有子集个数为( )
的所有子集个数为( )