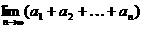22.(本小题满分12分)
已知函数f(x)=-x3+ax2+b(a, b∈R).
(Ⅰ)若a=1,函数f(x)的图象能否总在直线y=b的下方?说明理由;
(Ⅱ)若函数f(x)在[0,2]上 是增函数,x=2是方程f(x)=0的一个根,求证:f(1)≤-2;
(Ⅲ)若函数f(x)图象上任意不同两点的连线的斜率小于1,求实数a的取值范围.
21.(本小题满分12分)
设x、y∈R,在直角坐标平面内,a=(x,y+2),b=(x,y-2),且|a|+|b|=8.
(Ⅰ)求点M(x , y)的轨迹C的方程;
(Ⅱ)过点(0,3)作直线l与曲线C交于A、B两点,若以AB为直径的圆过坐标原点,求直线l的方程.
20.(本小题满分12分)
已知等差数列{an}的首项a1=1,且公差d>0,其第二项、第五项、第十四项分别是等比数列{bn}的第二项、第三项、第四项.
(Ⅰ)求数列{an}与{bn}的通项公式
(Ⅱ)设数列{cn}对任意自然数n均有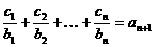 成立,
成立,
求 的值.
的值.
19.(本小题满分12分)
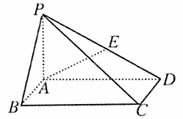
如图,在底面是矩形的四棱锥P-ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2.
(Ⅰ)求证:平面PDC⊥平面PAD;
(Ⅱ)若E是PD的中点,求异面直线AE与PC所成角的余弦值;
(Ⅲ)在BC边上是否存在一点G,使得D点到平面PAG的距离为1,若存在,求出BG的值;若不存在,请说明理由.
18.(本小题满分12分)
甲、乙、丙三人参加某项考试,合格的概率分别为
(Ⅰ)求三人中至少有两人合格的概率;
(Ⅱ)设三人中合格的人数为ξ,求ξ的数学期望.
17.(本小题满分12分)
已知函数f(x)=sin(x+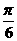 )+sin(x-
)+sin(x-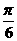 )+cosx+a(a∈R,a为常数).
)+cosx+a(a∈R,a为常数).
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)若函数f(x)在[-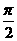 ,
,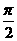 ] 上的最大值与最小值之和为
] 上的最大值与最小值之和为 ,求实数a的值.
,求实数a的值.
16.对任意的函数f(x), g(x),在公共定义域内,规定f(x)*g(x)=min{f(x), g(x)} (min{f(x), g(x)}为f(x)与g(x)中最小的一个),若f(x)=lg(3-x), g(x)=lg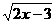 ,则f(x)*g(x)的最大值为
.
,则f(x)*g(x)的最大值为
.

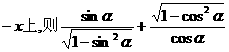 的值等于 ( )
的值等于 ( ) ,经过这3个点的小圆的周长为4π,则这个球的半径为
.
,经过这3个点的小圆的周长为4π,则这个球的半径为
.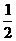 为公比的无穷等比数列,则
为公比的无穷等比数列,则