5. 甲、乙两个乒乓球运动员进行乒乓球单打比赛，已知每一局甲获胜的概率为0.6，乙获胜的概率为0.4。

　　 (1)赛满3局，甲胜2局的概率是多少？

　　 (2)若比赛采用三局二胜制，先赢两局为胜，求甲获胜的概率。

4. 已知A、B、C为三个相互独立事件，若事件A发生的概率为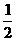，事件B发生的概率为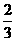，事件C发生的概率为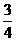，求下列事件的概率：

　　 (1)事件A、B、C都不发生；

　　 (2)事件A、B、C不都发生；

　　 (3)事件A发生且B、C恰好发生一个

3. 对同一目标进行3次射击，第1、第2、第3次射击的命中概率分别为0.4、0.5、0.7，求：

　　 (1)在这3次射击中，恰好有1次击中目标的概率；

　　 (2)在这3次射击中，至少有1次击中目标的概率。

2. 一个自动报警器由雷达和计算机两个部分组成，两部分有任何一个失灵，这个报警器就失灵。若使用100小时后，雷达部分失灵的概率为0.1，计算机失灵的概率为0.3，若两部分失灵与否是独立的，求这个报警器使用100小时而不失灵的概率。

1. 一次投掷两颗骰子，求出现的点数之和为奇数的概率。

18．满足z+2i(－z)+2＝0且arg(z－2)＝的复数是否存在？若存在，求出z；若不存在，请说明理由。

18．满足z+2i(－z)+2＝0且arg(z－2)＝的复数是否存在？若存在，求出z；若不存在，请说明理由。

高中三年级　　　　　 班 学号　　　　　 　姓名　　　　　　　　　　　　　　　　　　　 　成绩　　　　　　　　　　　　　　　　 .

17．设，ω＝z+ai, (a∈R), z＝,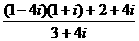

　　　　 (1) 求z的三角形式；

　　　　 (2) 当0≤a≤3时，求|ω|的取值范围；

　　　　 (3) 当|ω|≤2时, 求argω的取值范围。

16．设z∈C，且|z－2|＝2, z+∈R，求z.