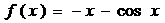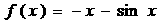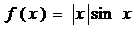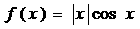6.
如图,一个半径为10米的水轮按逆时针方向每分钟转4圈.记水轮上的点P到水面的距离为d米(P在水面下则d为负数),则d(米)与时间t(秒)之间满足关系式: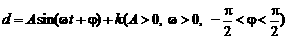 ,且当P点从水面上浮现时开始计算时间.有以下四个结论:
,且当P点从水面上浮现时开始计算时间.有以下四个结论:
①A=10; ②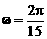 ; ③
; ③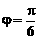 ; ④k=5.
; ④k=5.
则其中所有正确结论的序号是 .
4.
设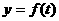 是某港口水的深度y(米)关于时间t(时)的函数,其中
是某港口水的深度y(米)关于时间t(时)的函数,其中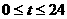 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
t |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观观察,函数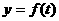 的图象可以近似地看成函数
的图象可以近似地看成函数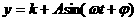 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是 ( )
(A)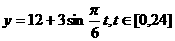 (B)
(B)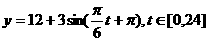
(C)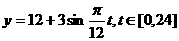 (D)
(D)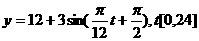
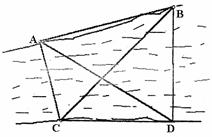
3. 如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得
∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离是( ).
(A)20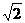 (B)20
(B)20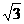 (C)40
(C)40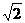 (D)20
(D)20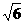
6.(1)将条件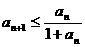 变形,得
变形,得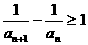 .
.
于是,有
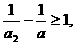
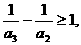
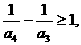
…………
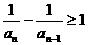 .
.
将这n-1个不等式叠加,得 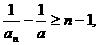
故 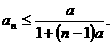
(2)注意到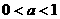 ,于是由(1)得
,于是由(1)得
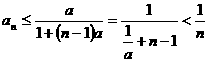 ,
,
从而,有 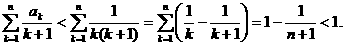
第三讲 三角函数
陕西特级教师 安振平
l 高考风向标
主要考查三角函数的定义,三角函数的符号,同角三角函数关系式及诱导公式,两角和与差的三角函数,二倍角的正弦、余弦、正切公式,三角函数的图象与性质,包括周期性、奇偶性、单调性、和最值性.
l 典型题选讲
例1 (1)已知: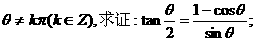
(2)已知: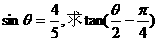 的值.
的值.
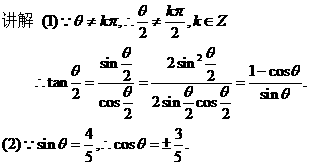
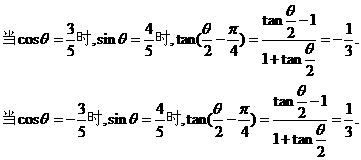
点评 三角问题的解决,变形是多途径的.例如:题1也可以逆向考虑,事实上
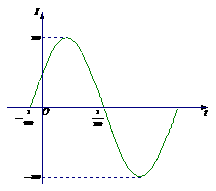
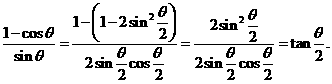
例2 已知电流I与时间t的关系式为 .
.
(1)右图是 (ω>0,
(ω>0,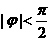 )
)
在一个周期内的图象,根据图中数据求
的解析式;
(2)如果t在任意一段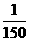 秒的时间内,电流
秒的时间内,电流 都能取得最大值和最小值,那么ω的最小正整数值是多少?
都能取得最大值和最小值,那么ω的最小正整数值是多少?
讲解 本小题主要考查三角函数的图象与性质等基础知识,考查运算能力和逻辑推理能力.
(1)由图可知 A=300.
设t1=-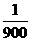 ,t2=
,t2=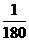 , 则周期T=2(t2-t1)=2(
, 则周期T=2(t2-t1)=2(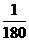 +
+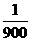 )=
)=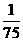 .
.
∴
ω=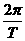 =150π.
=150π.
又当t=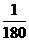 时,I=0,即sin(150π·
时,I=0,即sin(150π·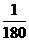 +
+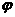 )=0,
)=0,
而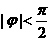 , ∴
, ∴ 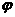 =
=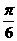 .
.
故所求的解析式为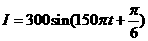 .
.
(2)依题意,周期T≤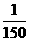 ,即
,即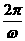 ≤
≤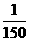 ,(ω>0)
,(ω>0)
∴ ω≥300π>942,又ω∈N*,
故最小正整数ω=943.
点评 本题解答的开窍点是将图形语言转化为符号语言.其中,读图、识图、用图是形数结合的有效途径.
例3 已知函数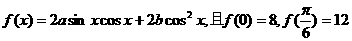 .
.
(1)求实数a,b的值;
(2)求函数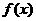 的最大值及取得最大值时x的值.
的最大值及取得最大值时x的值.
(1)函数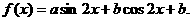
讲解 学会翻译,逐步展开解题思维.
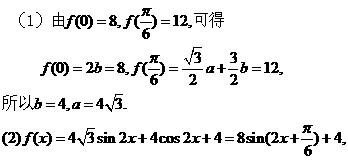
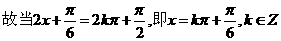 时,函数f(x)的最大值为12.
时,函数f(x)的最大值为12.
点评 结论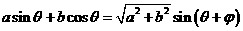 是历年高考命题的热点之一.
是历年高考命题的热点之一.
例4 已知tan2θ=-2,π<2θ<2π,求.
讲解
解题目标中含有角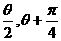 ,可向
,可向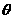 角转化,以便出现
角转化,以便出现 ;而条件中的
;而条件中的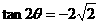 可向
可向 转化. 这样,就消除了解题目标与解题条件之间中的差异.事实上
转化. 这样,就消除了解题目标与解题条件之间中的差异.事实上
原式= = = , 由 tan2θ=, 解得 tanθ=-或tanθ=, ∵π<2θ<2π,∴<θ<π, ∴tanθ=- , ∴原式==3+2.
点评 差异分析,有时需要从条件和解题目标两个方向同时进行分析,这种相向而行的思维方式,可以快速联结解题的思维线路.
例5 在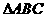 中,
中,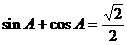 ,
,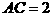 ,
,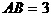 ,求
,求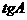 的值和
的值和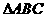 的面积.
的面积.
讲解 本题是2004年北京高考试题,下面给出两种解法.
法一 先解三角方程,求出角A的值.
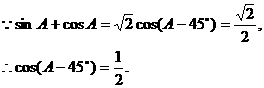
又 ,
,
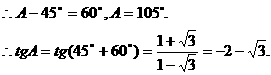
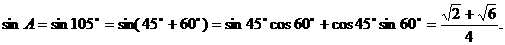
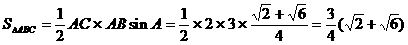 .
.
法二 由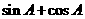 计算它的对偶关系式
计算它的对偶关系式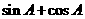 的值.
的值.
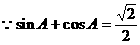 ①
①
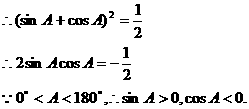
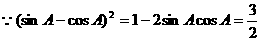 ,
,
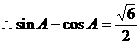 . ②
. ②
① + ② 得 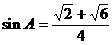 .
.
① - ② 得 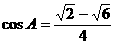 .
.
从而 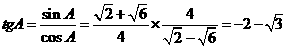 .以下解法略去.
.以下解法略去.
点评 本小题主要考查三角恒等变形、三角形面积公式等基本知识,着重数学考查运算能力,是一道三角的基础试题.两种解法比较起来,你认为哪一种解法比较简单呢?
例6 设函数f(x)=a·b,其中向量a=(2cosx,1),b=(cosx, 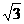 sin2x),x∈R.
sin2x),x∈R.
(1)若f(x)=1-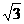 且x∈[-
且x∈[-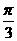 ,
,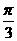 ],求x;
],求x;
(2)若函数y=2sin2x的图象按向量c=(m,n)(|m|<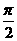 )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.
讲解 (1)依题设可知,函数的解析式为
f(x)=a·b=2cos2x+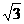 sin2x=1+2sin(2x+
sin2x=1+2sin(2x+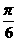 ).
).
由1+2sin(2x+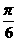 )=1-
)=1-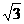 ,可得三角方程
,可得三角方程
sin(2 x
+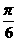 )=-
)=-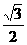 .
.
∵-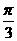 ≤x≤
≤x≤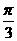 ,
,
∴-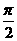 ≤2x+
≤2x+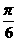 ≤
≤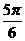 ,
,
∴2x+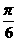 =-
=-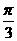 ,即x=-
,即x=-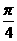 .
.
(2)函数y=2sin2x的图象按向量c=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,即函数y=f(x)的图象.
由(1)得
f(x)=2sin2(x+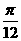 )+1.
)+1.
∵|m|<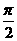 ,∴
,∴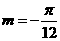 ,
,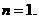
点评 本小题是2004年福建高考试题,主要考查平面向量的概念和计算,三角函数的恒等变换及其图象变换的基本技能,着重考查数学运算能力.平面向量与三角函数结合是高考命题的一个新的亮点之一.
例7 已知向量m=(1,1),向量n与向量m夹角为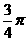 ,且m·n=-1.
,且m·n=-1.
(1)求向量n;
(2)若向量n与向量q=(1,0)的夹角为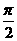 ,向量p=
,向量p=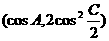 ,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求|n+p|的取值范围.
,其中A、C为△ABC的内角,且A、B、C依次成等差数列.求|n+p|的取值范围.
讲解 (1)设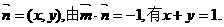 ①
①
 与
与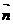 夹角为
夹角为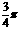 ,有
,有 ·
·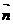 =|
=| |·|
|·|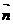 |·
|·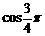 ,
,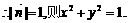 ②
②
由①②解得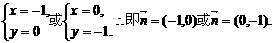
(2)由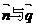 垂直知
垂直知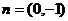 ,
,
由2B=A+C 知B=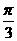 ,A+C=
,A+C=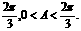
若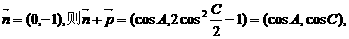
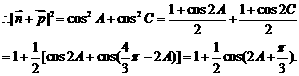
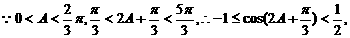
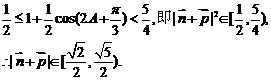
点评 本题的特色是将向量与三角综合,体现了知识的交汇性.解题后,请你反思:解题思维的入手点,解题思维的障碍点,解题思维的开窍点,只有这样的反思训练,请相信,你就会慢慢成为解题高手的.
例8 如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=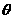 ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
(1)用a,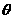 表示S1和S2;
表示S1和S2;
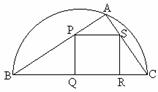 (2)当a固定,
(2)当a固定,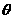 变化时,求
变化时,求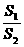 取最小值时的角
取最小值时的角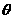 .
.
讲解 (1)∵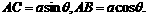
∴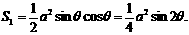
设正方形边长为x.
则BQ=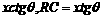
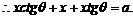
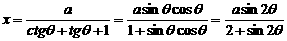
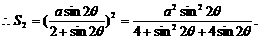
(2)当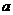 固定,
固定,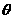 变化时,
变化时,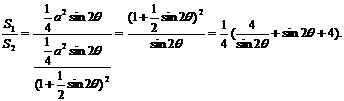
令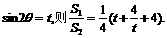
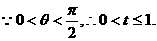 令
令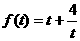 任取
任取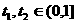 ,且
,且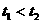 ,
,
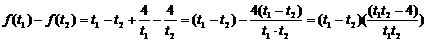 .
.
 ,
,
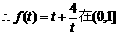 是减函数.
是减函数.
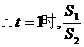 取最小值,此时
取最小值,此时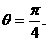
点评 三角函数有着广泛的应用,本题就是一个典型的范例.通过引入角度,将图形的语言转化为三角的符号语言,再通过局部的换元,又将问题转化为我们熟知的函数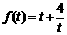 .这些解题思维的拐点,你能否很快的想到呢?
.这些解题思维的拐点,你能否很快的想到呢?
l 针对性演练

 求
求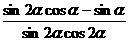 的值.
的值.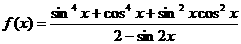 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.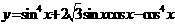 的最小正周期和最小值;并写出该函数在
的最小正周期和最小值;并写出该函数在 上的单调递增区间.
上的单调递增区间.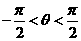 ,且
,且 其中
其中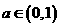 ,则关于
,则关于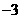 (B)3 或
(B)3 或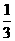
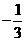 (D)
(D)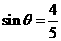 ,且
,且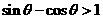 ,则
,则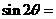 ( )
( )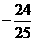 (B)
(B)
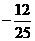 (C)
(C)
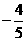 (D)
(D) 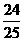
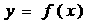 的图象如图所示,则
的图象如图所示,则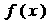 的解析式可能是
( )
的解析式可能是
( )
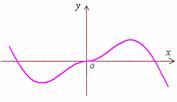 (A)
(A)