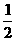6. 给出平面区域如图,若使目标函数z=x+ay (a>0),取得最大值的最优解有无数个,则a的一个可能的取值为 ( )
(A)1 (B)3 (C)-1 (D)-3
5.已知:双曲线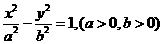 ,其右支上的一点p,F1,F2为其两焦点,则△F1F2的内切圆在x轴上的切点Q的坐标
(
)
,其右支上的一点p,F1,F2为其两焦点,则△F1F2的内切圆在x轴上的切点Q的坐标
(
)
A、(b,0)
B、(a,0)
C、(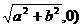 D、不确定
D、不确定
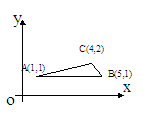
1. 若非空集合A={x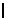 2a+1≤x≤3a-5},B={x|3≤x≤22},则能使AÍA
2a+1≤x≤3a-5},B={x|3≤x≤22},则能使AÍA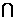 B成立的所有a的集合是
( )
A、{a|1≤a≤9} B、{a|6≤a≤9} C、{a|a≤9} D、
B成立的所有a的集合是
( )
A、{a|1≤a≤9} B、{a|6≤a≤9} C、{a|a≤9} D、
22. (本大题满分14分)
已知△OPQ的面积为S,且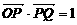 ,
,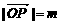 ,
,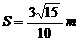 ,以O为中心,P为焦点的椭圆经过点Q.
(1)当m
,以O为中心,P为焦点的椭圆经过点Q.
(1)当m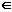 (0,2)时,求
(0,2)时,求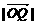 的最小值,并求出此时的椭圆C方程;
(2)在(1)的条件下,过点P的直线l与椭圆C相交于M、N两点,与椭圆C对应于焦点P的准线相交于D点,且
的最小值,并求出此时的椭圆C方程;
(2)在(1)的条件下,过点P的直线l与椭圆C相交于M、N两点,与椭圆C对应于焦点P的准线相交于D点,且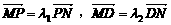 ,证明
,证明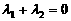 .
.
21. (本大题满分12分) 已知f (x)=2ax-4x3 (x∈[0,1]),222233是否存在正整数a,使f (x)的图象的最高点落在直线y=12上?若存在,求出a的值;若不存在,请说明理由.
20. (本大题满分12分)
某种商品在30天内的销售价格P(元)与时间t (天)的函数关系用右图的两条线段表示,该商品在30天内日销售量Q (件)与时间t (天)之间函数关系为Q=40-t (0<t≤30,t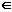 N*).
(1)写出该商品的销售价格P与时间t的函数关系式;
(2)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(日销售金额=销售价格×日销售量).
N*).
(1)写出该商品的销售价格P与时间t的函数关系式;
(2)求该商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?(日销售金额=销售价格×日销售量).
19. 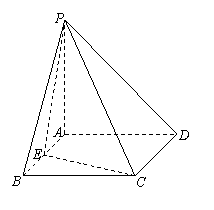 (本大题满分12分)
在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=6,BC=3,DC=
(本大题满分12分)
在直角梯形P1DCB中,P1D∥CB,CD⊥P1D,P1D=6,BC=3,DC=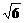 ,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
(1)求证PA⊥平面ABCD;
(2)求平面PEC和平面PAD所成的二面角(锐角)的大小.
,A是P1D的中点,E是线段AB的中点,沿AB把平面P1AB折起到平面PAB的位置,使二面角P-CD-B成45°角.
(1)求证PA⊥平面ABCD;
(2)求平面PEC和平面PAD所成的二面角(锐角)的大小.


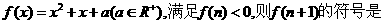 ( )
( )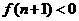 B、
B、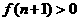 C、
C、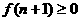 D、
D、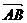 =
=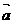 ,
, ,
,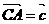 边长为1,则
边长为1,则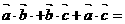 ( )
( )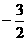 B、
B、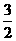 C、
C、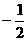 D、
D、