2025年活动单导学课程高中化学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年活动单导学课程高中化学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
6. (拓展)空间利用率的计算方法。
将原子(离子)设想为一个球,依据晶胞内所含原子(离子)的数目计算原子(离子)的体积,再确定晶胞的体积,即可计算晶体(胞)的空间利用率。
$空间利用率 = \frac{晶胞含有原子(离子)的体积}{晶胞体积} × 100\%$
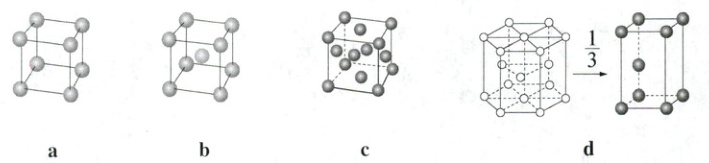
(1)简单立方堆积的空间利用率为
(2)体心立方堆积的空间利用率为
(3)面心立方堆积的空间利用率为
(4)六方堆积的空间利用率为
将原子(离子)设想为一个球,依据晶胞内所含原子(离子)的数目计算原子(离子)的体积,再确定晶胞的体积,即可计算晶体(胞)的空间利用率。
$空间利用率 = \frac{晶胞含有原子(离子)的体积}{晶胞体积} × 100\%$

(1)简单立方堆积的空间利用率为
52%
(保留整数,下同)。(2)体心立方堆积的空间利用率为
68%
。(3)面心立方堆积的空间利用率为
74%
。(4)六方堆积的空间利用率为
74%
。
答案:
6.
(1)52%
(2)68%
(3)74%
(4)74%
解析:
(1)在简单立方堆积(如图所示)中,1个晶胞中含有1个金属原子,设立方体的边长为a,原子半径为r,则晶胞体积为$a^{3}$,金属原子的半径$r=\frac{a}{2}$,则空间利用率=$\frac{\frac{4\pi}{3}r^{3}}{a^{3}}×100\%=\frac{\pi}{6}×100\%\approx52\%$。
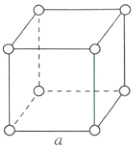
(2)在体心立方堆积(如图所示)中,设立方体的边长为a,原子半径为r,则体对角线长度=$\sqrt{3}a=4r$,而1个晶胞中含有2个金属原子,则空间利用率=$\frac{2×\frac{4\pi}{3}r^{3}}{a^{3}}×100\%=\frac{\frac{8\pi}{3}r^{3}}{(\frac{4r}{\sqrt{3}})^{3}}×100\%=\frac{\sqrt{3}\pi}{8}×100\%\approx68\%$。
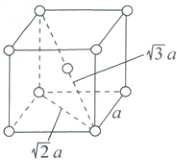
(3)在面心立方堆积(如图所示)中,设晶胞边长为a,原子半径为r,则面对角线长度=$\sqrt{2}a=4r$,$a=2\sqrt{2}r$,1个晶胞中含有4个金属原子,则空间利用率=$\frac{4×\frac{4}{3}\pi r^{3}}{a^{3}}=\frac{\frac{16\pi}{3}r^{3}}{(2\sqrt{2}r)^{3}}×100\%=\frac{\pi}{3\sqrt{2}}×100\%\approx74\%$。
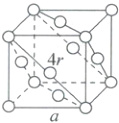
(4)在六方堆积(如图所示)中,设原子半径为r,则底面边长为2r,底面高$h_{1}=\sqrt{3}r$,所以底面积$S=2r×\sqrt{3}r=2\sqrt{3}r^{2}$。设正三棱锥的高为$h_{2}$,则$(\frac{2}{3}h_{1})^{2}+h_{2}^{2}=4r^{2}$,已知$h_{1}=\sqrt{3}r$,则$h_{2}=\frac{2\sqrt{6}}{3}r$,该晶胞的高$h=2h_{2}=2×\frac{2\sqrt{6}}{3}r$,所以晶胞体积$V_{晶胞}=S× h=2\sqrt{3}r^{2}×\frac{4\sqrt{6}}{3}r=8\sqrt{2}r^{3}$,1个晶胞中含有2个金属原子,则空间利用率=$\frac{2×\frac{4}{3}\pi r^{3}}{8\sqrt{2}r^{3}}×100\%=\frac{\pi}{3\sqrt{2}}×100\%\approx74\%$。

6.
(1)52%
(2)68%
(3)74%
(4)74%
解析:
(1)在简单立方堆积(如图所示)中,1个晶胞中含有1个金属原子,设立方体的边长为a,原子半径为r,则晶胞体积为$a^{3}$,金属原子的半径$r=\frac{a}{2}$,则空间利用率=$\frac{\frac{4\pi}{3}r^{3}}{a^{3}}×100\%=\frac{\pi}{6}×100\%\approx52\%$。

(2)在体心立方堆积(如图所示)中,设立方体的边长为a,原子半径为r,则体对角线长度=$\sqrt{3}a=4r$,而1个晶胞中含有2个金属原子,则空间利用率=$\frac{2×\frac{4\pi}{3}r^{3}}{a^{3}}×100\%=\frac{\frac{8\pi}{3}r^{3}}{(\frac{4r}{\sqrt{3}})^{3}}×100\%=\frac{\sqrt{3}\pi}{8}×100\%\approx68\%$。

(3)在面心立方堆积(如图所示)中,设晶胞边长为a,原子半径为r,则面对角线长度=$\sqrt{2}a=4r$,$a=2\sqrt{2}r$,1个晶胞中含有4个金属原子,则空间利用率=$\frac{4×\frac{4}{3}\pi r^{3}}{a^{3}}=\frac{\frac{16\pi}{3}r^{3}}{(2\sqrt{2}r)^{3}}×100\%=\frac{\pi}{3\sqrt{2}}×100\%\approx74\%$。

(4)在六方堆积(如图所示)中,设原子半径为r,则底面边长为2r,底面高$h_{1}=\sqrt{3}r$,所以底面积$S=2r×\sqrt{3}r=2\sqrt{3}r^{2}$。设正三棱锥的高为$h_{2}$,则$(\frac{2}{3}h_{1})^{2}+h_{2}^{2}=4r^{2}$,已知$h_{1}=\sqrt{3}r$,则$h_{2}=\frac{2\sqrt{6}}{3}r$,该晶胞的高$h=2h_{2}=2×\frac{2\sqrt{6}}{3}r$,所以晶胞体积$V_{晶胞}=S× h=2\sqrt{3}r^{2}×\frac{4\sqrt{6}}{3}r=8\sqrt{2}r^{3}$,1个晶胞中含有2个金属原子,则空间利用率=$\frac{2×\frac{4}{3}\pi r^{3}}{8\sqrt{2}r^{3}}×100\%=\frac{\pi}{3\sqrt{2}}×100\%\approx74\%$。

7. (拓展)计算金属晶体的密度、晶胞质量、阿伏加德罗常数。
求晶胞的质量:$m = \frac{NM}{N_A}$,$N$表示晶胞中平均含有的金属原子数,$M$表示金属的摩尔质量,$N_A$表示阿伏加德罗常数。
求金属晶体的密度:$\rho = \frac{m}{V}$,$V$表示晶胞的体积。
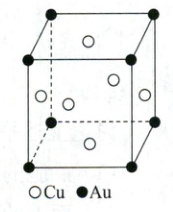
例:已知金属间可以形成合金,金和铜可以形成多种合金晶体。其中一种的晶体结构如图所示(为面心立方结构)。
(1)该金属化合物的化学式为
(2)已知$Au$的相对原子质量为 197,$Cu$的相对原子质量为 64,阿伏加德罗常数为$N_A mol^{-1}$,若该合金的密度为$d g/cm^3$,试计算两个最近金原子的核间距。
求晶胞的质量:$m = \frac{NM}{N_A}$,$N$表示晶胞中平均含有的金属原子数,$M$表示金属的摩尔质量,$N_A$表示阿伏加德罗常数。
求金属晶体的密度:$\rho = \frac{m}{V}$,$V$表示晶胞的体积。
例:已知金属间可以形成合金,金和铜可以形成多种合金晶体。其中一种的晶体结构如图所示(为面心立方结构)。
(1)该金属化合物的化学式为
AuCu3
。(2)已知$Au$的相对原子质量为 197,$Cu$的相对原子质量为 64,阿伏加德罗常数为$N_A mol^{-1}$,若该合金的密度为$d g/cm^3$,试计算两个最近金原子的核间距。

答案:
7.
(1)$AuCu_{3}$
(2)两个最近金原子的核间距=晶胞的棱长=$\sqrt[3]{\frac{(64×3 + 197)g/mol}{N_{A}mol^{-1}× dg/cm^{3}}}=\sqrt[3]{\frac{389}{N_{A}· d}}cm$。
解析:
(1)处于顶点的粒子为8个晶胞共有,每个原子有$\frac{1}{8}$属于该晶胞,则$Au$原子数=$8×\frac{1}{8}=1$;处于面上的粒子,同时为两个晶胞共有,每个原子有$\frac{1}{2}$属于该晶胞,则$Cu$原子数=$6×\frac{1}{2}=3$;原子数比$N(Cu):N(Au)=3:1$,则化学式为$AuCu_{3}$。
(2)晶胞体积$V=\frac{m}{\rho}=\frac{M}{d· N_{A}}=a^{3}$(设a为棱长),则$a=\sqrt[3]{\frac{M}{d· N_{A}}}$。
(1)$AuCu_{3}$
(2)两个最近金原子的核间距=晶胞的棱长=$\sqrt[3]{\frac{(64×3 + 197)g/mol}{N_{A}mol^{-1}× dg/cm^{3}}}=\sqrt[3]{\frac{389}{N_{A}· d}}cm$。
解析:
(1)处于顶点的粒子为8个晶胞共有,每个原子有$\frac{1}{8}$属于该晶胞,则$Au$原子数=$8×\frac{1}{8}=1$;处于面上的粒子,同时为两个晶胞共有,每个原子有$\frac{1}{2}$属于该晶胞,则$Cu$原子数=$6×\frac{1}{2}=3$;原子数比$N(Cu):N(Au)=3:1$,则化学式为$AuCu_{3}$。
(2)晶胞体积$V=\frac{m}{\rho}=\frac{M}{d· N_{A}}=a^{3}$(设a为棱长),则$a=\sqrt[3]{\frac{M}{d· N_{A}}}$。
查看更多完整答案,请扫码查看


