2026年拔尖特训五年级数学上册北师大版广东专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年拔尖特训五年级数学上册北师大版广东专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
(1)(昭通威信)有$3$个真分数:$\frac{a}{50},\frac{b}{34},\frac{c}{19}$。
在这$3$个数中,(
(
在这$3$个数中,(
$\frac{c}{19}$
)一定是最简真分数,(
$\frac{a}{50}$
)一定能化成有限小数。
答案:
1.(1)$\frac{c}{19}$ $\frac{a}{50}$
(2)(南京鼓楼区)$a$,$b$均为非零自然数。若
$a ÷ b = 4$,则$a$和$b$的最大公因数是(
若$a - b = 1$,则$a$和$b$的最小公倍数是(
$a ÷ b = 4$,则$a$和$b$的最大公因数是(
$b$
);若$a - b = 1$,则$a$和$b$的最小公倍数是(
$ab$
)。
答案:
(2)$b$ $ab$ 解析:$a,b$均为非零自然数,若$a ÷ b=4$,则$a$和$b$为倍数关系,$a$是$b$的$4$倍,则$a$和
(2)$b$ $ab$ 解析:$a,b$均为非零自然数,若$a ÷ b=4$,则$a$和$b$为倍数关系,$a$是$b$的$4$倍,则$a$和
(3)(丽水松阳)一个分数,先用$2$约分一次,再用
$3$约分一次后是$\frac{2}{3}$。这个分数原来是(
$3$约分一次后是$\frac{2}{3}$。这个分数原来是(
$\frac{12}{18}$
)。
答案:
(3)$\frac{12}{18}$
(3)$\frac{12}{18}$
(4)(深圳南山区)如图,涂色部分的面积占
整个图形面积的(
整个图形面积的(
$\frac{1}{8}$
)。
答案:
(4)$\frac{1}{8}$
(4)$\frac{1}{8}$
(5)(茂名)两根绳子分别长$45$分米和$63$分
米,要把它们剪成同样长的小段且没有剩余,
则每小段最长为(
米,要把它们剪成同样长的小段且没有剩余,
则每小段最长为(
$9$
)分米。
答案:
(5)$9$
(5)$9$
(6)(茂名)已知两个自然数的差是$5$,它们的
最小公倍数与最大公因数的差是$203$,则这两
个数的和是(
最小公倍数与最大公因数的差是$203$,则这两
个数的和是(
$29$
)。
答案:
(6)$29$ 解析:分情况讨论:①如果两个数有公因数$5$,那么它们的最小公倍数也是$5$的倍数,最小公倍数与最大公因数的差一定是$5$的倍数,显然$203$不是$5$的倍数,所以这种情况不符合题意;
②当这两个数互质时,互质的两个数的最大公因数是$1$,所以这两个数的最小公倍数是$203+1=204$。根据互质的两个数的最小公倍数是它们的乘积,把$204$分解质因数,再结合这两个数的差是$5$即可解答。
(6)$29$ 解析:分情况讨论:①如果两个数有公因数$5$,那么它们的最小公倍数也是$5$的倍数,最小公倍数与最大公因数的差一定是$5$的倍数,显然$203$不是$5$的倍数,所以这种情况不符合题意;
②当这两个数互质时,互质的两个数的最大公因数是$1$,所以这两个数的最小公倍数是$203+1=204$。根据互质的两个数的最小公倍数是它们的乘积,把$204$分解质因数,再结合这两个数的差是$5$即可解答。
(7)(济南)一个最简分数,分子与分母的和
是$86$,如果分子与分母都减去$9$,得到的分数
是$\frac{8}{9}$,那么原来的分数是(
是$86$,如果分子与分母都减去$9$,得到的分数
是$\frac{8}{9}$,那么原来的分数是(
$\frac{41}{45}$
)。
答案:
(7)$\frac{41}{45}$ 解析:原来的分数的分子与分母的和是$86$,如果分子与分母都减去$9$,新得到的分数的分子与分母的和是$86-9 × 2=68$,新得到的分数约分后是$\frac{8}{9}$,那么原来的分数的分母是$68 ÷ (9+8) × 9+9=45$,分子是$86-45=41$。
(7)$\frac{41}{45}$ 解析:原来的分数的分子与分母的和是$86$,如果分子与分母都减去$9$,新得到的分数的分子与分母的和是$86-9 × 2=68$,新得到的分数约分后是$\frac{8}{9}$,那么原来的分数的分母是$68 ÷ (9+8) × 9+9=45$,分子是$86-45=41$。
(1)(深圳龙岗区)笑笑$8$分做了$5$朵纸花,
淘气$9$分做了$7$朵同样的纸花。两人的速度
相比,(
A.笑笑做得快
B.淘气做得快
C.一样快
D.无法比较
淘气$9$分做了$7$朵同样的纸花。两人的速度
相比,(
B
)。A.笑笑做得快
B.淘气做得快
C.一样快
D.无法比较
答案:
2.(1)B
(2)(深圳龙岗区)$\frac{3}{5}$的分子加$9$,要使它的大
小不变,分母应该(
A.加$9$
B.乘$9$
C.乘$3$
D.加$15$
小不变,分母应该(
D
)。A.加$9$
B.乘$9$
C.乘$3$
D.加$15$
答案:
(2)D
(2)D
(3)(深圳龙华区)如图,梯形下底的长度是上底的$3$倍,则涂色部分的面积占梯形面积的(
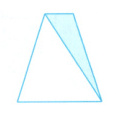
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$
C
)。
A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{1}{5}$
答案:
(3)C
(3)C
(4)(深圳罗湖区)一个最简真分数,分子与
分母的积是$36$,这样的分数有(
A.$1$
B.$2$
C.$3$
D.$4$
分母的积是$36$,这样的分数有(
B
)个。A.$1$
B.$2$
C.$3$
D.$4$
答案:
(4)B 解析:先列举出$36$的因数,再一一组成分数,选出其中的最简真分数。
(4)B 解析:先列举出$36$的因数,再一一组成分数,选出其中的最简真分数。
3. (北京海淀区)大课间同学们玩“抱团”游戏,
人数在$20$和$30$之间。同学们发现当“抱团”
口令中所报的数为$3$,$4$和$6$时,每个人都可
以“抱团”成功。有多少人在玩游戏?

人数在$20$和$30$之间。同学们发现当“抱团”
口令中所报的数为$3$,$4$和$6$时,每个人都可
以“抱团”成功。有多少人在玩游戏?

答案:
3.$3,4$和$6$的公倍数有$12,24,36,48,· · ·$
因为人数在$20$和$30$之间,所以有$24$人在玩游戏
因为人数在$20$和$30$之间,所以有$24$人在玩游戏
4. (怀化辰溪)一堆桃子,$3$个$3$个地数多$1$个,
$5$个$5$个地数也多$1$个,$7$个$7$个地数还是多
$1$个。这堆桃子至少有多少个?
$5$个$5$个地数也多$1$个,$7$个$7$个地数还是多
$1$个。这堆桃子至少有多少个?
答案:
4.$3,5,7$的最小公倍数是$3 × 5 × 7=105$
$105+1=106(个)$ 解析:只要求出$3,5,7$的最小公倍数,再加上$1$即可得解。
$105+1=106(个)$ 解析:只要求出$3,5,7$的最小公倍数,再加上$1$即可得解。
查看更多完整答案,请扫码查看


