《2026年拔尖特训五年级数学上册北师大版广东专版》

1. 白棋每次跳 2 格，请用“$□$”标记出白棋跳到的位置；黑棋每次跳 5 格，请用“$◯$”标记出黑棋跳到的位置。

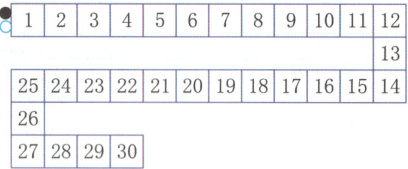
$♀$1 2 3 4 5 6 7 8 9 10 11 12 13
25 24 23 22 21 20 19 18 17 16 15 14
26
27 28 29 30
既标有“$□$”又标有“$◯$”的有(10,20,30)。

答案： 1. 用“$□ $”标记的数:2,4,6,8,10,12,14,16,18, 20,22,24,26,28,30
用“$◯$”标记的数:5,10,15,20,25,30 10,20,30

2. 把 50 以内 4 和 5 的倍数、公倍数分别填在下面的圈内，再找出 4 和 5 的最小公倍数。
50 以内 4 的倍数 50 以内 5 的倍数

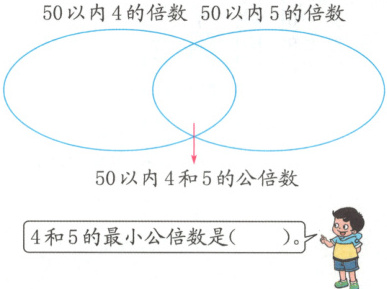
4 和 5 的最小公倍数是(20)。

答案：
2. 20

3. 写出下面每组数的最小公倍数，并说说你的发现。
7 和 13
(91)
11 和 16
(176)
20 和 21
(420)
8 和 56
(56)
5 和 25
(25)
17 和 51
(51)
我发现：当两个数的最大公因数是(1)时，这两个数的最小公倍数是(两数的乘积)；当两个数中较大数是较小数的(倍数)时，这两个数的最小公倍数是(较大数)。

答案： 3. 91　176　420　56　25　51　1
两数的乘积　倍数　较大数

4. ★写出下面各组分数中分母的最小公倍数。
$\frac{7}{8}$和$\frac{3}{10}$(40)
$\frac{5}{12}$和$\frac{3}{8}$(24)
$\frac{2}{15}$和$\frac{5}{12}$(60)
$\frac{7}{9}$和$\frac{8}{21}$(63)

答案： 4. 40　24　60　63
方法归纳
求两个数的最小公倍数的方法
方法一:列举法,先分别写出两个数各自的倍数,再从中找出它们的最小公倍数。
方法二:试除法,先写出较大数的倍数,再用这些数按从小到大的顺序依次除以较小数,第一个除以较小数没有余数的数就是它们的最小公倍数。

5. 填一填。
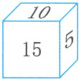
(1)$A = 2 × 3 × 5$，$B = 2 × 2 × 5$，$A$和$B$的最大公因数是(10)，最小公倍数是(60)。
(2)如图所示的正方体的每个面上都有一个非零自然数，相对两个面上的自然数的乘积相同，则这个正方体上的六个数的和最小是(41)。

答案： 5.
(1)10　60　
(2)41

6. (生活体验)欢欢和乐乐都利用暑假时间去游泳馆游泳，欢欢每 3 天去一次，乐乐每 4 天去一次，7 月的最后一天两人正好同时去游泳，最快几月几日他们又同时去游泳?

答案： 6. 8月12日
解析:3和4的最小公倍数是12,7月的最后一天是7月31日，再过12天，即8月12日。

7. (传统文化)天干地支，简称“干支”，取义于树木的干和枝。天干有十：甲、乙、丙、丁、戊、己、庚、辛、壬、癸；地支有十二：子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。将十个天干和十二个地支按顺序两两相配，刚好能组成一甲子(60 年)，你能解释其中的缘由吗?

答案： 7. 天干十个，地支十二个，两者的最小公倍数是六十,也就是十个天干和十二个地支按顺序两两相配,共能配成60组，即一甲子

8. (思维过程)有一批巧克力，如果每 24 块装一盒，那么最后一盒差 2 块；如果每 28 块装一盒，那么最后一盒也差 2 块；如果每 32 块装一盒，那么最后一盒只有 30 块。这批巧克力最少一共有多少块?

答案： 8. 因为$24=2×2×2×3,28=2×2×7,32=2×2×2×2×2$,所以24,28,32的最小公倍数是$2×2×2×2×2×3×7=672$ $672 - 2 = 670$(块)
解析:先求出24，28，32的最小公倍数，如果每24块装一盒，那么最后一盒差2块;如果每28块装一盒，那么最后一盒也差2块;如果每32块装一盒,那么最后一盒只有30块,即最后一盒同样差2块，所以用它们的最小公倍数减去2即可解答。