1. 将$\frac{5}{7}$变为$\frac{50}{70}$,分数的大小(
不变
)。
答案:
不变
2. $\frac{2}{5}$的分母加上 10,要使分数的大小不变,分子应加上(
4
)。
答案:
4
3. 用分数表示涂色部分。
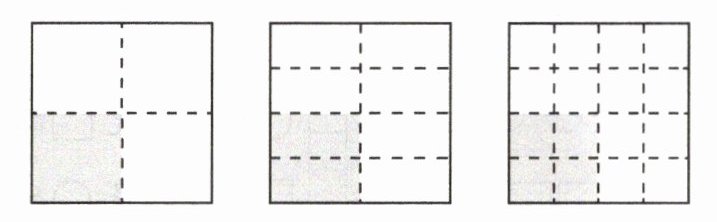
(
这三个数的大小为

(
$\frac{1}{4}$
)($\frac{2}{8}$
)($\frac{3}{12}$
)这三个数的大小为
$\frac{1}{4}=\frac{2}{8}=\frac{3}{12}$
,由此可知,分数的分子和分母同时(乘
)或(除以
)同一个不为零的数,分数的大小(不变
)。
答案:
$\frac{1}{4}$;$\frac{2}{8}$;$\frac{3}{12}$;$\frac{1}{4}=\frac{2}{8}=\frac{3}{12}$;乘;除以;不变
二、在括号里填上适当的数。
$\frac{6}{48}=\frac{6÷6}{48÷(
$\frac{3}{4}=\frac{3×5}{(
$1\frac{1}{2}=\frac{(
$\frac{6}{48}=\frac{6÷6}{48÷(
6
)}=\frac{(1
)}{(8
)}$$\frac{3}{4}=\frac{3×5}{(
4
)×(5
)}=\frac{(15
)}{(20
)}$$1\frac{1}{2}=\frac{(
3
)}{2}=\frac{(3
)×(8
)}{(2
)×(8
)}=\frac{24}{(16
)}$
答案:
6,1,8;4,5,15,20;3,3,8,2,8,16
三、小法官判案。
1. $\frac{4}{5}$里有 8 个$\frac{1}{10}$。(
2. $\frac{3}{4}=\frac{3+3}{4+3}=\frac{6}{7}$(
3. 分数单位相同,分数的大小不一定相等。(
1. $\frac{4}{5}$里有 8 个$\frac{1}{10}$。(
√
)2. $\frac{3}{4}=\frac{3+3}{4+3}=\frac{6}{7}$(
×
)3. 分数单位相同,分数的大小不一定相等。(
√
)
答案:
√×√
四、下面哪些分数在直线上能用同一个点表示?在直线上把它们表示出来。
$\frac{2}{12}$ $\frac{1}{3}$ $\frac{4}{24}$ $\frac{3}{18}$ $\frac{2}{5}$

$\frac{2}{12}$ $\frac{1}{3}$ $\frac{4}{24}$ $\frac{3}{18}$ $\frac{2}{5}$

答案:
$\frac{2}{12}$、$\frac{4}{24}$、$\frac{3}{18}$ 能用同一个点表示。
1.
你能把$\frac{2}{3}$和$\frac{3}{5}$化成分母是 30 而分数大小不变的分数吗?


你能把$\frac{2}{3}$和$\frac{3}{5}$化成分母是 30 而分数大小不变的分数吗?


答案:
$\frac{2}{3}=\frac{2×10}{3×10}=\frac{20}{30}$
$\frac{3}{5}=\frac{3×6}{5×6}=\frac{18}{30}$
$\frac{3}{5}=\frac{3×6}{5×6}=\frac{18}{30}$
2. 结合下面的算式,画图说明分数的基本性质。
$\frac{1}{4}=\frac{1×2}{4×2}=\frac{2}{8}$
$\frac{1}{4}=\frac{1×2}{4×2}=\frac{2}{8}$
答案:
画一条长方形(或圆形)表示单位“1”,将其平均分成4份,取其中1份涂色表示$\frac{1}{4}$;
用相同大小的长方形(或圆形),平均分成8份,取其中2份涂色表示$\frac{2}{8}$;
通过观察图形,可看到$\frac{1}{4}$与$\frac{2}{8}$所占整体的大小相同,即$\frac{1}{4}=\frac{1×2}{4×2}=\frac{2}{8}$。
用相同大小的长方形(或圆形),平均分成8份,取其中2份涂色表示$\frac{2}{8}$;
通过观察图形,可看到$\frac{1}{4}$与$\frac{2}{8}$所占整体的大小相同,即$\frac{1}{4}=\frac{1×2}{4×2}=\frac{2}{8}$。
六、快乐提升。
一个分数,分子、分母同时除以相同的数得$\frac{6}{7}$,原来分子与分母的和是 52。原来的分数是多少?
一个分数,分子、分母同时除以相同的数得$\frac{6}{7}$,原来分子与分母的和是 52。原来的分数是多少?
答案:
答:设原来分数分子分母同时除以的数为$k$($k\neq0$),原来分子为$6k$,分母为$7k$。
可列方程$6k + 7k = 52$,
即$13k = 52$,
解得$k = 4$。
原来分子为$6×4 = 24$,
原来分母为$7×4 = 28$。
所以原来的分数是$\frac{24}{28}$。
可列方程$6k + 7k = 52$,
即$13k = 52$,
解得$k = 4$。
原来分子为$6×4 = 24$,
原来分母为$7×4 = 28$。
所以原来的分数是$\frac{24}{28}$。
查看更多完整答案,请扫码查看


