1. $24 = 1×24 = (
$30 = 1×30 = (
24 的全部因数:(
30 的全部因数:(
(
2
)×(12
) = (3
)×(8
) = (4
)×(6
)$$30 = 1×30 = (
2
)×(15
) = (3
)×(10
) = (5
)×(6
)$24 的全部因数:(
1,2,3,4,6,8,12,24
)30 的全部因数:(
1,2,3,5,6,10,15,30
)(
1,2,3,6
)既是 24 的因数,又是 30 的因数。
答案:
1. $2×12$;$3×8$;$4×6$;
$2×15$;$3×10$;$5×6$;
$1,2,3,4,6,8,12,24$;
$1,2,3,5,6,10,15,30$;
$1,2,3,6$
$2×15$;$3×10$;$5×6$;
$1,2,3,4,6,8,12,24$;
$1,2,3,5,6,10,15,30$;
$1,2,3,6$
2. 18 的因数有(
1,2,3,6,9,18
),这些因数中,是偶数的数有(2,6,18
),是奇数的数有(1,3,9
)。
答案:
1,2,3,6,9,18;2,6,18;1,3,9
3. (
1、3、9
)既是 9 的因数,又是 18 的因数。
答案:
1、3、9
二、小法官判案。
1. 3 的因数只有 1 个。 ( )
2. 一个数越大因数越多。 ( )
3. 一个数的因数一定比这个数小。 ( )
4. 51 的因数只有 1 和 51。 ( )
5. 20 的因数有无数个。 ( )
1. 3 的因数只有 1 个。 ( )
2. 一个数越大因数越多。 ( )
3. 一个数的因数一定比这个数小。 ( )
4. 51 的因数只有 1 和 51。 ( )
5. 20 的因数有无数个。 ( )
答案:
×
@@×
@@×
@@×
@@×
@@×
@@×
@@×
@@×
三、在圈里填上合适的数。
12 的因数 27 的因数
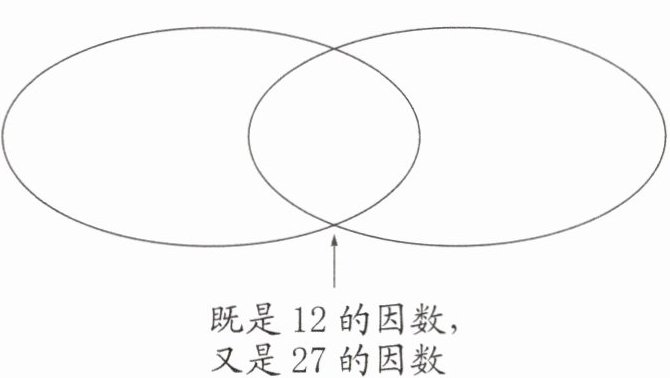
12 的因数 27 的因数

12的因数圈填1、2、3、4、6、12;27的因数圈填1、3、9、27;重叠部分填1、3。
答案:
12的因数圈填1、2、3、4、6、12;27的因数圈填1、3、9、27;重叠部分填1、3。
1. 食品厂生产了 1500 个面包,选用下面哪种包装可以正好装完?


答案:
1500 ÷ 15 = 100(盒)
1500 ÷ 25 = 60(盒)
1500 ÷ 35 ≈ 42.86(盒)
因为1500能被15和25整除,不能被35整除,所以选用第一种或第二种包装可以正好装完。
1500 ÷ 25 = 60(盒)
1500 ÷ 35 ≈ 42.86(盒)
因为1500能被15和25整除,不能被35整除,所以选用第一种或第二种包装可以正好装完。
2. 淘淘收集了 36 只昆虫标本,把它们分格摆放,要求每格摆放昆虫标本的只数相同,且多于 2 只少于 8 只,可以分成多少格?
答案:
因为每格摆放昆虫标本的只数相同,且多于2只少于8只,36的因数有:1、2、3、4、6、9、12、18、36。
满足多于2只少于8只的因数有:3、4、6。
当每格摆3只时,格数为:$36÷3 = 12$(格)
当每格摆4只时,格数为:$36÷4 = 9$(格)
当每格摆6只时,格数为:$36÷6 = 6$(格)
答:可以分成12格或9格或6格。
满足多于2只少于8只的因数有:3、4、6。
当每格摆3只时,格数为:$36÷3 = 12$(格)
当每格摆4只时,格数为:$36÷4 = 9$(格)
当每格摆6只时,格数为:$36÷6 = 6$(格)
答:可以分成12格或9格或6格。
五、快乐提升。
新学期开始后,李老师领来 123 本书,恰好平均分给了五(1)班的同学们。你知道五(1)班有多少个同学吗?请说出你的理由。
新学期开始后,李老师领来 123 本书,恰好平均分给了五(1)班的同学们。你知道五(1)班有多少个同学吗?请说出你的理由。
答案:
123的因数有1、3、41、123。
因为班级人数通常大于1且小于123,所以可能的人数为3或41。
结合实际情况,一个班级41人更合理。
答:五
(1)班有41个同学。
因为班级人数通常大于1且小于123,所以可能的人数为3或41。
结合实际情况,一个班级41人更合理。
答:五
(1)班有41个同学。
查看更多完整答案,请扫码查看


