《2025年同步导学与优化训练五年级数学上册北师大版》

1. $6.\dot{4}\dot{5}$保留两位小数是(6.45),保留三位小数是(6.455)。

答案： 6.45，6.455

2. $9.45353…$是(循环)小数,循环节是(53),用简便记法表示为($9.4\dot{5}\dot{3}$)。

答案： 循环；53；$9.4\dot{5}\dot{3}$

3. 把$238.75÷0.25$转化为除数是整数的除法算式是($23875÷25$),这是根据(商不变)的性质。

答案： $23875÷25$，商不变；

4. 在$2.\dot{9}7\dot{8}$,$2.9\dot{7}\dot{8}$,$2.97$,$2.97878…$这四个数中,最大的是($2.\dot{9}7\dot{8}$),最小的是($2.97$),相等的是($2.9\dot{7}\dot{8}$)和($2.97878…$)。

答案： 最大的是$2.\dot{9}7\dot{8}$，最小的是$2.97$，相等的是$2.9\dot{7}\dot{8}$和$2.97878…$

5. 不用计算,说说结果是偶数还是奇数。
$146 + 348$(偶数) $3267 + 154$(奇数)
$77×65$(奇数) $2375 - 321$(偶数)
$364×157$(偶数) $436 - 351$(奇数)

答案： (偶数)，(奇数)，(奇数)，(偶数)，(偶数)，(奇数)

1. 用竖式计算并验算。
$1.89÷0.54 = $3.5 $4.2÷0.4 = $10.5

答案：

2. 用简便方法计算。
$4.57×1.2 - 4.57×0.2$
$44.8÷(44.8÷0.8)$

答案： 第一题：$4.57×1.2 - 4.57×0.2$
解：
$=4.57×(1.2 - 0.2)$
$=4.57×1$
$=4.57$
第二题：$44.8÷(44.8÷0.8)$
解：
$=44.8÷44.8×0.8$
$=1×0.8$
$=0.8$

三、画一画。

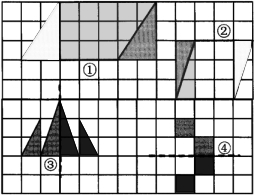
1. 图①中的三角形向右平移5格,原来的平行四边形变成了( )形。
2. 图②中的三角形向左平移3格,原来的平行四边形变成了( )形。
3. 以虚线为对称轴,画出图③、图④的轴对称图形。

答案：

1. 一个书包$63.7$元,一个笔盒$9.8$元,李阿姨带了$100$元去买了1个书包,剩下的钱买笔盒,她最多能买几个笔盒？

答案： 1. 计算买书包后剩余的钱：$100 - 63.7 = 36.3$（元）
2. 计算最多能买笔盒的数量：$36.3 ÷ 9.8 \approx 3.704$
3. 由于笔盒个数为整数，向下取整得$3$个
答：她最多能买$3$个笔盒。

2. 某工程队要修一条路,计划每天修$1.6\mathrm{km}$,$25$天修完,实际每天比计划多修$0.4\mathrm{km}$,实际多少天修完？

答案： 1. 这条路的总长度：$1.6×25=40$（km）
2. 实际每天修的长度：$1.6+0.4=2$（km）
3. 实际修完需要的天数：$40÷2=20$（天）
答：实际20天修完。