第40页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
12. 打雷时雷声和闪电是同时发生的,但我们总是先看见闪电后听到雷声,原因是光在空气中的传播速度
大于
(选填“小于”“大于”或“等于”)声音在空气中的传播速度;雷声是由空气
的振动产生的,人看见闪电 3 s 后听到雷声,则人与闪电处的距离大约为1020
m。
答案:
大于 空气 1020
13. 2023 年 7 月 30 日,第 31 届世界大学生夏季运动会(后简称成都大运会)男子 25 米手枪速射团体决赛在四川成都举行,中国队荣获冠军。这是中国队在成都大运会射击比赛中的首金。运动员在射击瞄准时需要做到“三点一线”,这是依据
光的直线传播
原理。比赛结束后,运动员们去公园游玩时,看见阳光透过树叶的缝隙在地上形成圆形光斑,这些光斑是太阳的实
(选填“虚”或“实”)像。
答案:
光的直线传播 实
14. 根据要求完成作图。
(1)室内一盏电灯通过木板隔墙上的两个小洞,透出两条细小光束(如下图甲所示)。请根据这两条光束的方向确定室内电灯的位置。
(2)请在图乙中画出物体 AB 在灯光下在地上形成的影子。
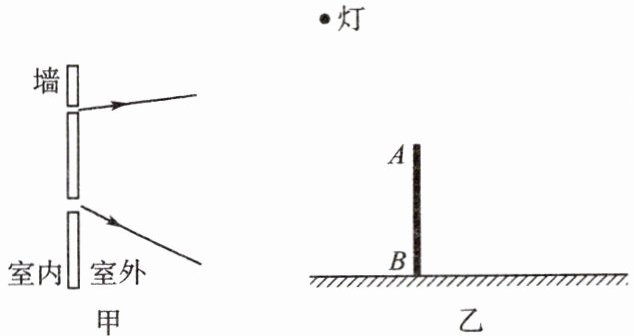
(1)室内一盏电灯通过木板隔墙上的两个小洞,透出两条细小光束(如下图甲所示)。请根据这两条光束的方向确定室内电灯的位置。
(2)请在图乙中画出物体 AB 在灯光下在地上形成的影子。

答案:
(1)
(2)
(1)

(2)

15. 小孔成像是光的直线传播的一个实例。北宋科学家沈括在《梦溪笔谈》中描述道:……“若鸢飞空中,其影随鸢而移;或中间为窗隙所束,则影与鸢遂相违,鸢东则影西,鸢西则影东。又如窗隙中楼塔之影,中间为窗所束,亦皆倒垂……”(如下图甲所示)某同学用硬纸筒探究小孔成像的原理,如图乙所示。
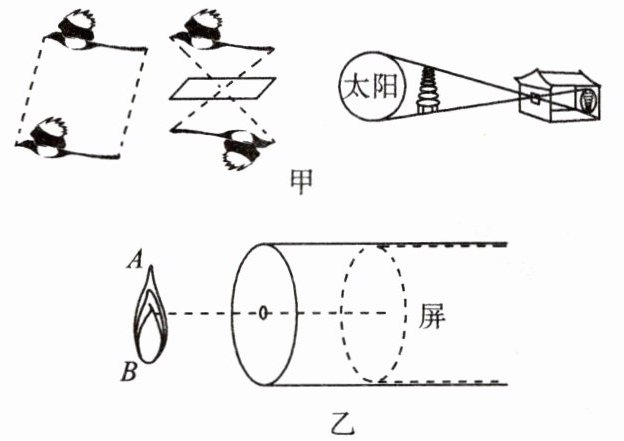
(1)请在图乙中作出烛焰 AB 在屏上所成的像 A'B'(要求标出 A'、B')。
(2)发现蜡烛和小孔的位置固定后,像离小孔越远,像就越大。他测出了像到小孔的不同距离时像的高度,填在下表中。
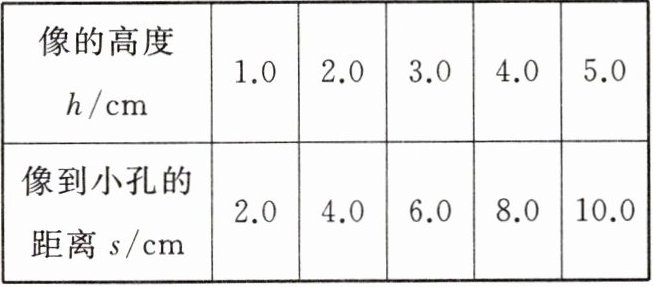
根据表中的数据可以得到的结论:蜡烛和小孔的位置固定后,像的高度 h 与像到小孔的距离 s 成_________(选填“正比”或“反比”)。
(3)小军知道树荫下的圆形光斑就是太阳通过树叶间的小孔在地面上成的像,他测出了光斑的直径为 2.8 cm,光斑到小孔的距离为 3.0 m,已知太阳到地球的距离为 $1.5×10^{11}$ m。由此可以估算出太阳的直径约为_________m。(结果保留整数)

(1)请在图乙中作出烛焰 AB 在屏上所成的像 A'B'(要求标出 A'、B')。
(2)发现蜡烛和小孔的位置固定后,像离小孔越远,像就越大。他测出了像到小孔的不同距离时像的高度,填在下表中。

根据表中的数据可以得到的结论:蜡烛和小孔的位置固定后,像的高度 h 与像到小孔的距离 s 成_________(选填“正比”或“反比”)。
(3)小军知道树荫下的圆形光斑就是太阳通过树叶间的小孔在地面上成的像,他测出了光斑的直径为 2.8 cm,光斑到小孔的距离为 3.0 m,已知太阳到地球的距离为 $1.5×10^{11}$ m。由此可以估算出太阳的直径约为_________m。(结果保留整数)
答案:
$(1)$
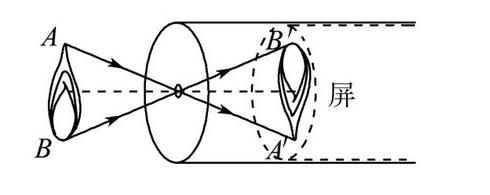
$(2)$ 分析像的高度 $h$ 与像到小孔的距离 $s$ 的关系
由表格中的数据:$\frac{h_{1}}{s_{1}}=\frac{1.0\mathrm{cm}}{2.0\mathrm{cm}} = 0.5$,$\frac{h_{2}}{s_{2}}=\frac{2.0\mathrm{cm}}{4.0\mathrm{cm}} = 0.5$,$\frac{h_{3}}{s_{3}}=\frac{3.0\mathrm{cm}}{6.0\mathrm{cm}} = 0.5$,$\frac{h_{4}}{s_{4}}=\frac{4.0\mathrm{cm}}{8.0\mathrm{cm}} = 0.5$,$\frac{h_{5}}{s_{5}}=\frac{5.0\mathrm{cm}}{10.0\mathrm{cm}} = 0.5$ ,即$\frac{h}{s}$为定值。
根据正比的定义:若两个量$x$、$y$满足$y = kx$($k$为常数),则$y$与$x$成正比。这里$h=\frac{1}{2}s$,所以像的高度 $h$ 与像到小孔的距离 $s$ 成正比 。
$(3)$ 计算太阳的直径
设太阳的直径为$D$,已知光斑直径$d = 2.8\mathrm{cm}=0.028\mathrm{m}$,光斑到小孔距离$s = 3.0\mathrm{m}$,太阳到地球距离$L = 1.5×10^{11}\mathrm{m}$。
根据相似三角形的性质(小孔成像的原理)可得$\frac{D}{L}=\frac{d}{s}$。
则$D=\frac{dL}{s}$,将数值代入可得:
$D=\frac{0.028\mathrm{m}×1.5× 10^{11}\mathrm{m}}{3.0\mathrm{m}}=1.4×10^{9}\mathrm{m}$
综上,答案依次为:$(2)$ 正比;$(3)$ $\boldsymbol{1.4× 10^{9}}$ 。
$(1)$

$(2)$ 分析像的高度 $h$ 与像到小孔的距离 $s$ 的关系
由表格中的数据:$\frac{h_{1}}{s_{1}}=\frac{1.0\mathrm{cm}}{2.0\mathrm{cm}} = 0.5$,$\frac{h_{2}}{s_{2}}=\frac{2.0\mathrm{cm}}{4.0\mathrm{cm}} = 0.5$,$\frac{h_{3}}{s_{3}}=\frac{3.0\mathrm{cm}}{6.0\mathrm{cm}} = 0.5$,$\frac{h_{4}}{s_{4}}=\frac{4.0\mathrm{cm}}{8.0\mathrm{cm}} = 0.5$,$\frac{h_{5}}{s_{5}}=\frac{5.0\mathrm{cm}}{10.0\mathrm{cm}} = 0.5$ ,即$\frac{h}{s}$为定值。
根据正比的定义:若两个量$x$、$y$满足$y = kx$($k$为常数),则$y$与$x$成正比。这里$h=\frac{1}{2}s$,所以像的高度 $h$ 与像到小孔的距离 $s$ 成正比 。
$(3)$ 计算太阳的直径
设太阳的直径为$D$,已知光斑直径$d = 2.8\mathrm{cm}=0.028\mathrm{m}$,光斑到小孔距离$s = 3.0\mathrm{m}$,太阳到地球距离$L = 1.5×10^{11}\mathrm{m}$。
根据相似三角形的性质(小孔成像的原理)可得$\frac{D}{L}=\frac{d}{s}$。
则$D=\frac{dL}{s}$,将数值代入可得:
$D=\frac{0.028\mathrm{m}×1.5× 10^{11}\mathrm{m}}{3.0\mathrm{m}}=1.4×10^{9}\mathrm{m}$
综上,答案依次为:$(2)$ 正比;$(3)$ $\boldsymbol{1.4× 10^{9}}$ 。
查看更多完整答案,请扫码查看


