第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
11. 下列光现象的成因,与射击比赛中“三点一线”的瞄准原理相同的是(
A.雨后彩虹
B.波光粼粼
C.海市蜃楼
D.形影不离
D
)A.雨后彩虹
B.波光粼粼
C.海市蜃楼
D.形影不离
答案:
D
12. 如图所示,小明用针孔照相机(即小孔成像实验装置)观察蜡烛的烛焰,若保持小孔和蜡烛的烛焰位置不变,则下列分析正确的是(
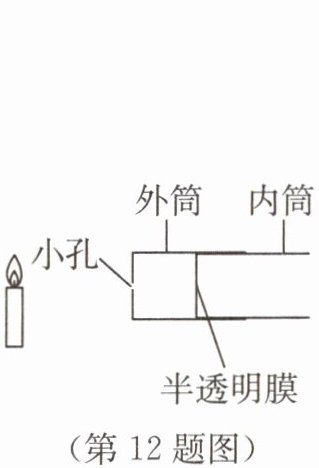
A.若内筒位置不变,则半透明膜上的像是正立的
B.若小孔改为小三角形,则半透明膜上的像也变为三角形
C.随着蜡烛的燃烧,半透明膜上的像也随之下移
D.若取下半透明膜,则透过小孔将看不到完整的烛焰
D
)
A.若内筒位置不变,则半透明膜上的像是正立的
B.若小孔改为小三角形,则半透明膜上的像也变为三角形
C.随着蜡烛的燃烧,半透明膜上的像也随之下移
D.若取下半透明膜,则透过小孔将看不到完整的烛焰
答案:
D
13. 沈括在《梦溪笔谈》中记述到“若鸢飞空中,其影随鸢而移”,图甲为这一现象的示意图;若在窗上开一个小孔,则在室内纸屏上也会看到“鸢的影子”,还会呈现“鸢西则影东”的现象,如图乙所示.“鸢西则影东”描述的现象叫
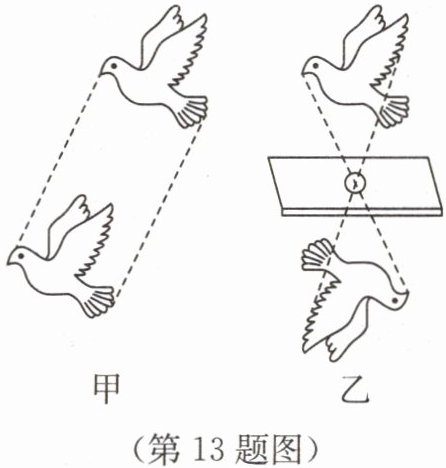
小孔成像
,图甲和图乙中的现象都可以用光的直线传播
来解释.
答案:
小孔成像;直线传播
14. 某同学用两个硬纸筒探究小孔成像,如图所示.
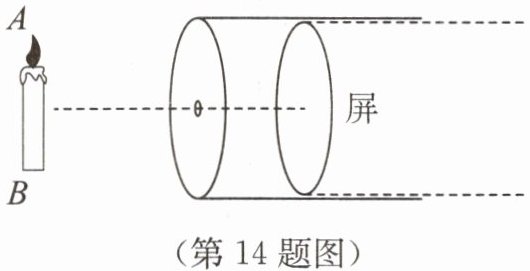
(1)实验过程中蜡烛燃烧不断缩短,导致光屏上烛焰的像向
(2)该同学发现蜡烛和小孔的位置固定后,像离小孔越远,像就越大.他测出了不同距离时像的高度,并将实验结果填在了下表中.根据表中的数据可以得到结论:蜡烛和小孔的位置固定后,像的高度$ h 与像到小孔的距离 s $的关系为
|像的高度$ h/cm $|1.0|2.0|3.0|4.0|5.0|
|像到小孔的距离$ s/cm $|2.0|4.0|6.0|8.0|10.0|


(1)实验过程中蜡烛燃烧不断缩短,导致光屏上烛焰的像向
上
(选填“上”或“下”)移动;若将蜡烛靠近小孔一些,则烛焰的像将变大
(选填“变大”“变小”或“不变”);若只将小圆孔改为三角形小孔,则像的形状不变
(选填“改变”或“不变”).(2)该同学发现蜡烛和小孔的位置固定后,像离小孔越远,像就越大.他测出了不同距离时像的高度,并将实验结果填在了下表中.根据表中的数据可以得到结论:蜡烛和小孔的位置固定后,像的高度$ h 与像到小孔的距离 s $的关系为
像的高度$h$与像到小孔的距离$s$成正比(或$h = 0.5s$)
.|像的高度$ h/cm $|1.0|2.0|3.0|4.0|5.0|
|像到小孔的距离$ s/cm $|2.0|4.0|6.0|8.0|10.0|

答案:
14.(1)上;变大;不变
(2)像的高度$h$与像到小孔的距离$s$成正比(或$h = 0.5s$)
(2)像的高度$h$与像到小孔的距离$s$成正比(或$h = 0.5s$)
查看更多完整答案,请扫码查看


