第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
16. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图.
|代表队|平均分/分|中位数/分|众数/分|方差/分^2|
|初中|a|85|b|$s^{2}_{初中}$|
|高中|85|c|100|160|
(1)根据图示计算出a,b,c的值;

(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差$s^{2}_{初中}$,并判断哪个队的选手成绩较为稳定.
|代表队|平均分/分|中位数/分|众数/分|方差/分^2|
|初中|a|85|b|$s^{2}_{初中}$|
|高中|85|c|100|160|
(1)根据图示计算出a,b,c的值;

(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差$s^{2}_{初中}$,并判断哪个队的选手成绩较为稳定.
答案:
(1)初中5名选手的成绩为:75、80、85、85、100。
$a=\frac{75 + 80 + 85 + 85 + 100}{5} = 85$(分)。
因为85出现的次数最多,所以$b = 85$。
高中5名选手的成绩为:70、75、80、100、100,将成绩从小到大排列为70、75、80、100、100,所以中位数$c = 80$。
(2)两队平均分都是85分。初中队中位数是85分,高中队中位数是80分。
因为85>80,在平均分相同的情况下,中位数高的初中队成绩更好些。
(3)$S_{初中}^{2}=\frac{1}{5}×\left[(75 - 85)^{2}+(80 - 85)^{2}+(85 - 85)^{2}+(85 - 85)^{2}+(100 - 85)^{2}\right]=\frac{1}{5}×(100 + 25 + 0 + 0 + 225)=\frac{1}{5}×350 = 70$。
已知$S_{高中}^{2}=160$,因为70<160,即$S_{初中}^{2}<S_{高中}^{2}$,所以初中队选手成绩较为稳定。
$a=\frac{75 + 80 + 85 + 85 + 100}{5} = 85$(分)。
因为85出现的次数最多,所以$b = 85$。
高中5名选手的成绩为:70、75、80、100、100,将成绩从小到大排列为70、75、80、100、100,所以中位数$c = 80$。
(2)两队平均分都是85分。初中队中位数是85分,高中队中位数是80分。
因为85>80,在平均分相同的情况下,中位数高的初中队成绩更好些。
(3)$S_{初中}^{2}=\frac{1}{5}×\left[(75 - 85)^{2}+(80 - 85)^{2}+(85 - 85)^{2}+(85 - 85)^{2}+(100 - 85)^{2}\right]=\frac{1}{5}×(100 + 25 + 0 + 0 + 225)=\frac{1}{5}×350 = 70$。
已知$S_{高中}^{2}=160$,因为70<160,即$S_{初中}^{2}<S_{高中}^{2}$,所以初中队选手成绩较为稳定。
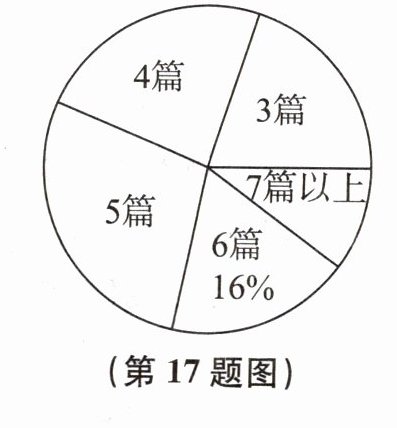
17. 某市自开展主题阅读活动以来,受到各校的广泛关注和同学们的积极响应,某校为了了解全校学生主题阅读的情况,随机抽查了部分学生某一周阅读主题文章的篇数,并绘制成统计图表.
|阅读文章/篇|3|4|5|6|7及以上|
|人数|20|28|m|16|12|
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和m的值;
(2)直接写出本次抽查的学生阅读文章篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生在这一周内阅读文章的篇数为4的人数.
|阅读文章/篇|3|4|5|6|7及以上|
|人数|20|28|m|16|12|
请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和m的值;
(2)直接写出本次抽查的学生阅读文章篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生在这一周内阅读文章的篇数为4的人数.

答案:
1. (1)
解:已知阅读$6$篇的人数为$16$人,占比$16\%$。
根据公式$总人数=\frac{部分人数}{部分人数占比}$,可得被抽查的学生人数为$\frac{16}{16\%}=100$人。
又因为$20 + 28+m + 16+12 = 100$,移项可得$m=100-(20 + 28+16+12)=100 - 76 = 24$。
2. (2)
众数是一组数据中出现次数最多的数据。
因为$28\gt24\gt20\gt16\gt12$,所以众数是$4$。
中位数:将$100$个数据从小到大排列,第$50$个和第$51$个数据的平均数为中位数。
前两组人数$20 + 28 = 48$,前三组人数$20 + 28+24 = 72$,所以第$50$个和第$51$个数据都在第三组(阅读$5$篇这一组),则中位数是$5$。
3. (3)
解:阅读文章篇数为$4$的人数占比为$\frac{28}{100}$。
该校共有$800$名学生,根据公式$估计人数=总人数×占比$,可得估计该校学生在这一周内阅读文章的篇数为$4$的人数为$800×\frac{28}{100}=224$人。
综上,(1)被抽查学生人数为$100$人,$m = 24$;(2)中位数是$5$,众数是$4$;(3)估计人数为$224$人。
解:已知阅读$6$篇的人数为$16$人,占比$16\%$。
根据公式$总人数=\frac{部分人数}{部分人数占比}$,可得被抽查的学生人数为$\frac{16}{16\%}=100$人。
又因为$20 + 28+m + 16+12 = 100$,移项可得$m=100-(20 + 28+16+12)=100 - 76 = 24$。
2. (2)
众数是一组数据中出现次数最多的数据。
因为$28\gt24\gt20\gt16\gt12$,所以众数是$4$。
中位数:将$100$个数据从小到大排列,第$50$个和第$51$个数据的平均数为中位数。
前两组人数$20 + 28 = 48$,前三组人数$20 + 28+24 = 72$,所以第$50$个和第$51$个数据都在第三组(阅读$5$篇这一组),则中位数是$5$。
3. (3)
解:阅读文章篇数为$4$的人数占比为$\frac{28}{100}$。
该校共有$800$名学生,根据公式$估计人数=总人数×占比$,可得估计该校学生在这一周内阅读文章的篇数为$4$的人数为$800×\frac{28}{100}=224$人。
综上,(1)被抽查学生人数为$100$人,$m = 24$;(2)中位数是$5$,众数是$4$;(3)估计人数为$224$人。
查看更多完整答案,请扫码查看


