第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
[对点训练2]小明同学从家步行去图书馆,他以5km/h的速度行进24min后,爸爸骑自行车以15km/h的速度按原路追赶小明.设爸爸出发xh后与小明会合,那么所列方程正确的是(
A.5(x+$\frac{24}{60}$)= 15x
B.5(x+24)= 15x
C.5x= 15(x+24)
D.5x= 15(x+$\frac{24}{60}$}
A
)A.5(x+$\frac{24}{60}$)= 15x
B.5(x+24)= 15x
C.5x= 15(x+24)
D.5x= 15(x+$\frac{24}{60}$}
答案:
A
1.解方程2(x-1)= 1时,去括号将其变形为
2x-2= 1的依据是(
A.乘法结合律
B.乘法分配律
C.等式性质1
D.等式性质2
2x-2= 1的依据是(
B
)A.乘法结合律
B.乘法分配律
C.等式性质1
D.等式性质2
答案:
B
2.《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何."设鸡有x只,可列方程为(
A.4x+2(94-x)= 35
B.4x+2(35-x)= 94
C.2x+4(94-x)= 35
D.2x+4(35-x)= 94
D
)A.4x+2(94-x)= 35
B.4x+2(35-x)= 94
C.2x+4(94-x)= 35
D.2x+4(35-x)= 94
答案:
D
3.小华同学在解方程5x-1= ( )x+3 时,把括号内的数看成了该数的相反数,解得x= 2,则该方程的正确解为x=
$\frac{1}{2}$
.
答案:
$\frac {1}{2}$
4.解方程:
(1)5x-3= 3x+15;
(2)2(3x-1)= -3(x+1).
(1)5x-3= 3x+15;
(2)2(3x-1)= -3(x+1).
答案:
解
(1)$5x-3=3x+15,$移项,得$5x-3x=15+3,$合并同类项,得$2x=18,$系数化为1,得$x=9.$
(2)$2(3x-1)=-3(x+1),$去括号,得$6x-2=-3x-3,$移项,得$6x+3x=-3+2,$合并同类项,得$9x=-1,$系数化为1,得$x=-\frac {1}{9}.$
(1)$5x-3=3x+15,$移项,得$5x-3x=15+3,$合并同类项,得$2x=18,$系数化为1,得$x=9.$
(2)$2(3x-1)=-3(x+1),$去括号,得$6x-2=-3x-3,$移项,得$6x+3x=-3+2,$合并同类项,得$9x=-1,$系数化为1,得$x=-\frac {1}{9}.$
5.将4个数a,b,c,d排成2行、2列,两边各加一
条大括号,记成|ac db|,定义|ac db|= ad-
bc,若|x-2x2 3|=2,则x=
条大括号,记成|ac db|,定义|ac db|= ad-
bc,若|x-2x2 3|=2,则x=
-2
.
答案:
-2
6.一艘船从甲码头顺流而行,用了3小时到达乙码头,该船从乙码头返回甲码头逆流而行,用了5小时,已知水流速度是3千米/时,则船在静水中的速度是
12
千米/时.(逆水速度= 静水速度一水流速度,顺水速度= 静水速度十水流速度)
答案:
12
7.某校组织七年级师生共300人乘车前往
“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当
天上午10:00便可以到达“故乡”农场,
但实际上他们当天上午9:40便到达了
“故乡”农场,已知汽车实际每小时行驶
的速度比原计划快10km.求汽车原计划行驶的速度.
(2)到达“故乡”农场后,需要购买门票,已知
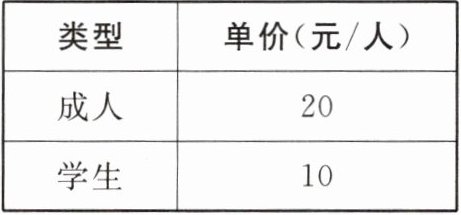
该农场门票票价情况,如表所示,该校购
买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
类型 单价(元/人)
成人 20
学生 10
“故乡”农场进行劳动教育活动.
(1)他们早晨8:00从学校出发,原计划当
天上午10:00便可以到达“故乡”农场,
但实际上他们当天上午9:40便到达了
“故乡”农场,已知汽车实际每小时行驶
的速度比原计划快10km.求汽车原计划行驶的速度.
(2)到达“故乡”农场后,需要购买门票,已知
该农场门票票价情况,如表所示,该校购
买门票时共花了3100元,那么参加此次劳动教育的教师、学生各多少人?
类型 单价(元/人)
成人 20
学生 10

答案:
解
(1)设汽车原计划行驶的速度是x km/h,则汽车实际行驶速度是$(x+10)km/h,$由题意得$2x=\frac {5}{3}(x+10)$,解得$x=50.$故汽车原计划行驶的速度为50 km/h.
(2)设参加此次劳动教育的教师有a人,则学生有(300 -a)人,由题意得$20a+10(300-a)=3100,$解得$a=10.$故参加此次劳动教育的教师有10人,学生有290人.
(1)设汽车原计划行驶的速度是x km/h,则汽车实际行驶速度是$(x+10)km/h,$由题意得$2x=\frac {5}{3}(x+10)$,解得$x=50.$故汽车原计划行驶的速度为50 km/h.
(2)设参加此次劳动教育的教师有a人,则学生有(300 -a)人,由题意得$20a+10(300-a)=3100,$解得$a=10.$故参加此次劳动教育的教师有10人,学生有290人.
查看更多完整答案,请扫码查看


