第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
知识点1 相反数的概念及代数意义
(1)只有
(2)0的相反数是
(3)一般地,a和
(1)只有
符号
不同的两个数,互为相反数.(2)0的相反数是
0
.(3)一般地,a和
-a
互为相反数,这里,a表示任意一个数,可以是正数、负数,也可以是0.
答案:
(1)符号;
(2)0;
(3)-a
(1)符号;
(2)0;
(3)-a
知识点2 相反数的几何意义
一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在

一般地,设a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在
正
、负
半轴上,表示a和-a(如图),这两个数只有符号不同.
答案:
正、负
【教材素材重现】你能借助数轴说明-(-a)= +a吗?
答案:
如图所示,-(-a)表示-a的相反数,是a,所以-(-a)=+a.

如图所示,-(-a)表示-a的相反数,是a,所以-(-a)=+a.

【例1】分别写出2,$-\frac{3}{2}$,$\frac{1}{2}$,-2.5的相反数,并在数轴上标出各数及它们的相反数,说明各对数在数轴上对应的点的位置特点.
答案:
解2的相反数是−2;−$\frac{3}{2}$的相反数是$\frac{3}{2}$;$\frac{1}{2}$的相反数是−$\frac{1}{2}$;−2.5的相反数是2.5.把这些数及它们的相反数表示在数轴上为2和−2,−$\frac{3}{2}$和$\frac{3}{2}$,$\frac{1}{2}$和−$\frac{1}{2}$,−2.5和2.5,各对数在数轴上对应的点分别位于原点两侧,且到原点的距离相等.

解2的相反数是−2;−$\frac{3}{2}$的相反数是$\frac{3}{2}$;$\frac{1}{2}$的相反数是−$\frac{1}{2}$;−2.5的相反数是2.5.把这些数及它们的相反数表示在数轴上为2和−2,−$\frac{3}{2}$和$\frac{3}{2}$,$\frac{1}{2}$和−$\frac{1}{2}$,−2.5和2.5,各对数在数轴上对应的点分别位于原点两侧,且到原点的距离相等.

【对点训练1】下列各组数中互为相反数的是(
A.+3和-(-3)
B.3和$\frac{1}{3}$
C.-2和$-\frac{1}{2}$
D.+(-4)和-(-4)
D
)A.+3和-(-3)
B.3和$\frac{1}{3}$
C.-2和$-\frac{1}{2}$
D.+(-4)和-(-4)
答案:
D
【例2】如图所示,点A,B,C,D表示的数中,表示互为相反数的两个点是(
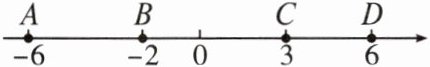
A.点A和点C
B.点B和点C
C.点A和点D
D.点B和点D
C
)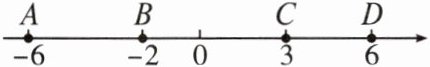
A.点A和点C
B.点B和点C
C.点A和点D
D.点B和点D
答案:
C
查看更多完整答案,请扫码查看


