2. 一台电视机,原来售价$ 1200 $元,现在的售价是$ 1080 $元。现在的售价比原来降低了百分之几?
答案:
降低的金额:1200 - 1080 = 120(元)
降低的百分比:120 ÷ 1200 × 100% = 10%
答:现在的售价比原来降低了10%。
降低的百分比:120 ÷ 1200 × 100% = 10%
答:现在的售价比原来降低了10%。
3. 某种水果,$ 3 月份第二周的价格比第一周涨了 20\% $,第三周的价格比第二周降了$ 20\% $。第三周的价格和第一周的价格相比,是涨了还是降了?变化幅度是多少?
答案:
设第一周价格为单位“1”。
第二周价格:$1×(1 + 20\%)=1.2$
第三周价格:$1.2×(1 - 20\%)=0.96$
$0.96<1$,降了。
变化幅度:$(1 - 0.96)÷1×100\% = 4\%$
答:第三周价格和第一周相比降了,变化幅度是4%。
第二周价格:$1×(1 + 20\%)=1.2$
第三周价格:$1.2×(1 - 20\%)=0.96$
$0.96<1$,降了。
变化幅度:$(1 - 0.96)÷1×100\% = 4\%$
答:第三周价格和第一周相比降了,变化幅度是4%。
4. 如图是学校图书室各类图书的统计图。
(1)学校图书室共有图书$ 600 $本,科技书有多少本?
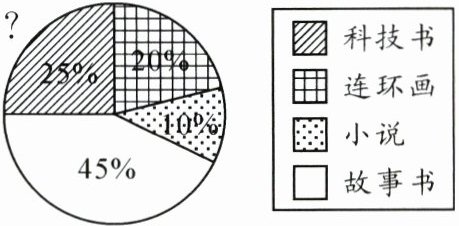
(2)故事书比连环画多几本?
(1)学校图书室共有图书$ 600 $本,科技书有多少本?

(2)故事书比连环画多几本?
答案:
(1) 600×25% = 150(本)
(2) 600×(45% - 20%) = 600×25% = 150(本)
(1) 600×25% = 150(本)
(2) 600×(45% - 20%) = 600×25% = 150(本)
5. 六年级甲、乙、丙三个班的学生参加捐款活动,其中乙班捐了$ 480 $元,占年级段总捐款数的$ \frac{3}{8} $,甲班捐款数和年级段总捐款数的比是$ 13:32 $,甲班捐款多少元?
答案:
1. 年级段总捐款数:$480÷\frac{3}{8}=480×\frac{8}{3}=1280$(元)
2. 甲班捐款数:$1280×\frac{13}{32}=520$(元)
答:甲班捐款520元。
2. 甲班捐款数:$1280×\frac{13}{32}=520$(元)
答:甲班捐款520元。
丁师傅加工一批零件,已完成个数与剩下个数的比是$ 1:4 $,如果丁师傅再加工$ 150 $个,刚好完成这批零件的一半。这批零件共有多少个?
答案:
设这批零件共有$x$个。
根据题意,最初完成的零件个数为$\frac{1}{5}x$,剩下的零件个数为$\frac{4}{5}x$(因为已完成个数与剩下个数的比是$1:4$,所以总份数为$1+4=5$)。
丁师傅再加工150个后,完成的零件个数变为$\frac{1}{5}x + 150$,此时刚好完成这批零件的一半,即$\frac{1}{2}x$。
因此,可以建立方程:
$\frac{1}{5}x + 150 = \frac{1}{2}x$,
移项得:
$\frac{1}{2}x - \frac{1}{5}x = 150$,
合并同类项得:
$\frac{3}{10}x = 150$,
系数化为1得:
$x = 500$。
所以,这批零件共有500个。
根据题意,最初完成的零件个数为$\frac{1}{5}x$,剩下的零件个数为$\frac{4}{5}x$(因为已完成个数与剩下个数的比是$1:4$,所以总份数为$1+4=5$)。
丁师傅再加工150个后,完成的零件个数变为$\frac{1}{5}x + 150$,此时刚好完成这批零件的一半,即$\frac{1}{2}x$。
因此,可以建立方程:
$\frac{1}{5}x + 150 = \frac{1}{2}x$,
移项得:
$\frac{1}{2}x - \frac{1}{5}x = 150$,
合并同类项得:
$\frac{3}{10}x = 150$,
系数化为1得:
$x = 500$。
所以,这批零件共有500个。
查看更多完整答案,请扫码查看


