2. 用递等式计算,能简算的要简算。
$ \frac{2}{5}+\frac{3}{5}×\frac{2}{3} $ $ (\frac{2}{3}-\frac{5}{18}+\frac{1}{2})÷\frac{1}{36} $ $ (\frac{3}{4}+\frac{1}{12})×\frac{3}{2} $
$ \frac{8}{15}×\frac{7}{4}+\frac{8}{15}÷4 $ $ (0.75+\frac{1}{2})×(\frac{5}{9}-\frac{1}{3}) $ $ \frac{17}{12}÷(3-\frac{12}{17}-\frac{5}{17}) $
$ \frac{2}{5}+\frac{3}{5}×\frac{2}{3} $ $ (\frac{2}{3}-\frac{5}{18}+\frac{1}{2})÷\frac{1}{36} $ $ (\frac{3}{4}+\frac{1}{12})×\frac{3}{2} $
$ \frac{8}{15}×\frac{7}{4}+\frac{8}{15}÷4 $ $ (0.75+\frac{1}{2})×(\frac{5}{9}-\frac{1}{3}) $ $ \frac{17}{12}÷(3-\frac{12}{17}-\frac{5}{17}) $
答案:
1.
$\quad\frac{2}{5} + \frac{3}{5} × \frac{2}{3}$
$ = \frac{2}{5} + \frac{2}{5} $
$= \frac{4}{5}$
2.
$\quad(\frac{2}{3} - \frac{5}{18} + \frac{1}{2}) ÷ \frac{1}{36} $
$= (\frac{12}{18} - \frac{5}{18} + \frac{9}{18}) × 36 $
$= \frac{16}{18} × 36 $
$ = 32$
3.
$\quad(\frac{3}{4} + \frac{1}{12}) × \frac{3}{2} $
$= (\frac{9}{12} + \frac{1}{12}) × \frac{3}{2} $
$= \frac{10}{12} × \frac{3}{2} $
$= \frac{5}{4}(或1.25)$
4.
$\quad\frac{8}{15} × \frac{7}{4} + \frac{8}{15} ÷ 4 $
$= \frac{8}{15} × \frac{7}{4} + \frac{8}{15} × \frac{1}{4} $
$= \frac{8}{15} × (\frac{7}{4} + \frac{1}{4}) $
$= \frac{8}{15} × 2 $
$= \frac{16}{15}(或1\frac{1}{15})$
5.
$\quad(0.75 + \frac{1}{2}) × (\frac{5}{9} - \frac{1}{3}) $
$= (\frac{3}{4} + \frac{2}{4}) × (\frac{5}{9} - \frac{3}{9}) $
$= \frac{5}{4} × \frac{2}{9} $
$= \frac{5}{18}$
6.
$\quad\frac{17}{12} ÷ (3 - \frac{12}{17} - \frac{5}{17}) $
$= \frac{17}{12} ÷ (3 - 1) $
$= \frac{17}{12} ÷ 2 $
$= \frac{17}{24}$
$\quad\frac{2}{5} + \frac{3}{5} × \frac{2}{3}$
$ = \frac{2}{5} + \frac{2}{5} $
$= \frac{4}{5}$
2.
$\quad(\frac{2}{3} - \frac{5}{18} + \frac{1}{2}) ÷ \frac{1}{36} $
$= (\frac{12}{18} - \frac{5}{18} + \frac{9}{18}) × 36 $
$= \frac{16}{18} × 36 $
$ = 32$
3.
$\quad(\frac{3}{4} + \frac{1}{12}) × \frac{3}{2} $
$= (\frac{9}{12} + \frac{1}{12}) × \frac{3}{2} $
$= \frac{10}{12} × \frac{3}{2} $
$= \frac{5}{4}(或1.25)$
4.
$\quad\frac{8}{15} × \frac{7}{4} + \frac{8}{15} ÷ 4 $
$= \frac{8}{15} × \frac{7}{4} + \frac{8}{15} × \frac{1}{4} $
$= \frac{8}{15} × (\frac{7}{4} + \frac{1}{4}) $
$= \frac{8}{15} × 2 $
$= \frac{16}{15}(或1\frac{1}{15})$
5.
$\quad(0.75 + \frac{1}{2}) × (\frac{5}{9} - \frac{1}{3}) $
$= (\frac{3}{4} + \frac{2}{4}) × (\frac{5}{9} - \frac{3}{9}) $
$= \frac{5}{4} × \frac{2}{9} $
$= \frac{5}{18}$
6.
$\quad\frac{17}{12} ÷ (3 - \frac{12}{17} - \frac{5}{17}) $
$= \frac{17}{12} ÷ (3 - 1) $
$= \frac{17}{12} ÷ 2 $
$= \frac{17}{24}$
3. 解方程。
$ x:\frac{7}{12}= \frac{3}{14} $ $ \frac{3}{7}x÷2= 6 $ $ \frac{2}{5}x+\frac{1}{4}x= 26 $
$ x:\frac{7}{12}= \frac{3}{14} $ $ \frac{3}{7}x÷2= 6 $ $ \frac{2}{5}x+\frac{1}{4}x= 26 $
答案:
$ x=\frac{1}{8} $;$ x=28 $;$ x=40 $
如图是一张机器人的行走路线图。
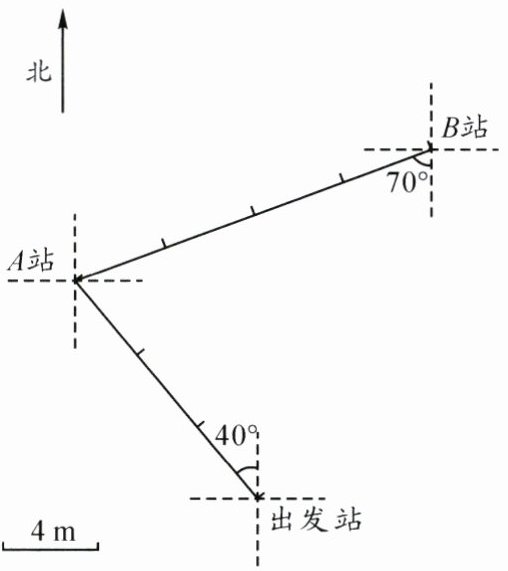
(1)机器人从出发站出发,先向(
(2)机器人最终的目的地是$ C $站。$ C 站位于 B 站南偏东 20^{\circ} 方向 16 $m处。请你在图上标出$ C $站的位置。
(3)如果机器人的行走速度为$ 2 $m/s,在每个站点需要停留$ 5 $s,那么机器人行完全程需要多少时间?

(1)机器人从出发站出发,先向(
西
)偏(北
)(40
)$ ^{\circ} $方向行走(12
)m到达$ A $站,接着向(东
)偏(北
)(70
)$ ^{\circ} $方向行走(16
)m到达$ B $站。(2)机器人最终的目的地是$ C $站。$ C 站位于 B 站南偏东 20^{\circ} 方向 16 $m处。请你在图上标出$ C $站的位置。
从$B$站出发,沿南偏东$20^{\circ}$方向,以$4m$为1个单位长度画$4$个单位长度,标出$C$站。
(3)如果机器人的行走速度为$ 2 $m/s,在每个站点需要停留$ 5 $s,那么机器人行完全程需要多少时间?
总路程:$12 + 16+16 = 44$($m$)
行走时间:$44÷2 = 22$($s$)
停留时间:$5×2 = 10$($s$)
总时间:$22 + 10 = 32$($s$)
答:机器人行完全程需要$32s$。
行走时间:$44÷2 = 22$($s$)
停留时间:$5×2 = 10$($s$)
总时间:$22 + 10 = 32$($s$)
答:机器人行完全程需要$32s$。
答案:
(1)西,北,40,12,东,北,70(或北,东,20),16
(2)从$B$站出发,沿南偏东$20^{\circ}$方向,以$4m$为1个单位长度画$4$个单位长度,标出$C$站。
(3)总路程:$12 + 16+16 = 44$($m$)
行走时间:$44÷2 = 22$($s$)
停留时间:$5×2 = 10$($s$)
总时间:$22 + 10 = 32$($s$)
答:机器人行完全程需要$32s$。
(1)西,北,40,12,东,北,70(或北,东,20),16
(2)从$B$站出发,沿南偏东$20^{\circ}$方向,以$4m$为1个单位长度画$4$个单位长度,标出$C$站。
(3)总路程:$12 + 16+16 = 44$($m$)
行走时间:$44÷2 = 22$($s$)
停留时间:$5×2 = 10$($s$)
总时间:$22 + 10 = 32$($s$)
答:机器人行完全程需要$32s$。
1. 小明看一本$ 180 $页的故事书,前$ 5 天看了 \frac{2}{3} $,第$ 6 $天应该从第几页开始看?
答案:
1. 计算前5天看的页数:$180×\frac{2}{3}=120$(页)
2. 第6天开始看的页数:$120+1=121$(页)
答:第6天应该从第121页开始看。
2. 第6天开始看的页数:$120+1=121$(页)
答:第6天应该从第121页开始看。
查看更多完整答案,请扫码查看


