《2025年综合学习与评估六年级数学上册人教版》

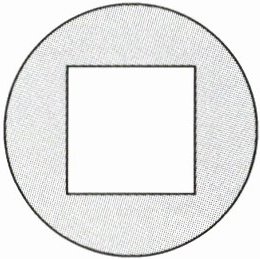
3. 安装在一种童车上的垫片的横截面如图所示,这张垫片的直径是 20 mm,中间有一个边长 10 mm 的正方形孔。这张垫片的横截面面积是多少？

答案： 圆的半径$r = 20÷2 = 10$（$mm$）。
圆的面积公式为$S = \pi r^{2}$，$\pi$取$3.14$，则圆的面积为：
$3.14×10^{2}=3.14×100 = 314$（$mm^{2}$）。
正方形的面积公式为$S = a^{2}$（$a$为正方形的边长），则正方形孔的面积为：
$10×10 = 100$（$mm^{2}$）。
垫片的横截面面积等于圆的面积减去正方形孔的面积，即：
$314 - 100 = 214$（$mm^{2}$）。
答：这张垫片的横截面面积是$214mm^{2}$。

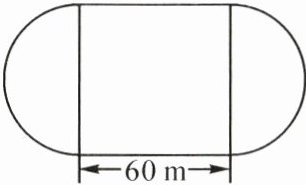
4. 如图,学校操场两端是半圆形,中间是正方形。这个操场的占地面积是多少平方米？张老师早上绕着操场跑了 3 圈,他一共跑了多少米？

答案： 占地面积 $6426$ 平方米，跑步总距离 $925.2$ 米。

5. 学校围绕一个半径 7 m 的圆形花坛铺一条 1 m 宽的大理石小路。如果每平方米大理石需要 150 元,铺这条大理石小路一共需要多少元？

答案： 外圆半径：$7 + 1 = 8$（m）。
外圆面积：$π × 8^2 = 64π$（$m^2$）。
内圆面积：$π × 7^2 = 49π$（$m^2$）。
小路面积（环形的面积）：$64π - 49π = 15π ≈ 47.1$（$m^2$）。
总费用：$47.1 × 150 = 7065$（元）。
答：铺这条大理石小路一共需要7065元。

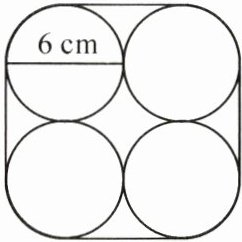
6. 超市搞活动,把 4 瓶圆柱形饮料用绳子捆扎在一起出售,横截面如图所示。如果接头部分用去 15 cm,一共需要多长的绳子？

答案： 绳子长度由四段圆弧和四条线段（直径长度）以及接头部分组成。
圆的直径为$6$cm，半径$r = 3$cm。
四段圆弧合起来刚好是一个圆的周长，根据圆的周长公式$C = 2\pi r$，可得圆周长为$2×3.14×3=18.84$cm。
四条线段长度为$4×6 = 24$cm。
再加上接头部分$15$cm。
所以绳子总长为$18.84 + 24 + 15 = 57.84$cm。
综上，一共需要$57.84$cm长的绳子。

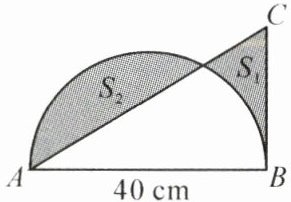
已知图中 $ S_{2} $ 比 $ S_{1} $ 多 $ 28 cm^{2} $,求 $ BC $ 的长。

答案： 设半圆的直径$AB$的中点为$O$，半圆半径$OA = OB = r$，
则$r = 40÷2 = 20cm$。
$S_{半圆}=\frac{1}{2}\pi r^{2}=\frac{1}{2}×3.14×20^{2}=628cm^{2}$。
因为$S_{2}+空白部分 = S_{半圆}$，$S_{1}+空白部分 = S_{\triangle ABC}$，$S_{2}-S_{1}=28cm^{2}$，
用$S_{半圆}-S_{\triangle ABC}=(S_{2}+空白部分)-(S_{1}+空白部分)=S_{2}-S_{1}=28cm^{2}$。
$S_{\triangle ABC}=\frac{1}{2}× AB× BC×=\frac{1}{2}×40× BC = 20BC$，
则$628 - 20BC=28$，
$20BC=628 - 28$，
$20BC = 600$，
$BC = 30cm$。
答：$BC$的长为$30cm$。