《2025年作业本浙江教育出版社三年级数学上册人教版》

(1) 一根绳子用去$\frac{1}{3}$米,还剩$\frac{2}{3}$米。这根绳子原来长( )米。

答案：
(1) $\frac{1}{3} + \frac{2}{3} = 1$（米）
所以这根绳子原来长 1 米。

(2) 计算$1-\frac{8}{9}$时,“1”可以看作( ),然后做减法。

答案：
(2) 在计算 $1 - \frac{8}{9}$ 时，可以将“1”看作 $\frac{9}{9}$，然后进行减法运算。
所以“1”可以看作 $\frac{9}{9}$。

(3) 加工同一种零件,张叔叔需用$\frac{1}{6}$小时,李叔叔需用$\frac{1}{5}$小时。两人同时开始加工,先完成任务的是( )。

答案：
(3) 张叔叔需要 $\frac{1}{6}$ 小时完成任务，李叔叔需要 $\frac{1}{5}$ 小时。
由于 $\frac{1}{6} ＜ \frac{1}{5}$，所以张叔叔先完成任务。
综上，先完成任务的是张叔叔。

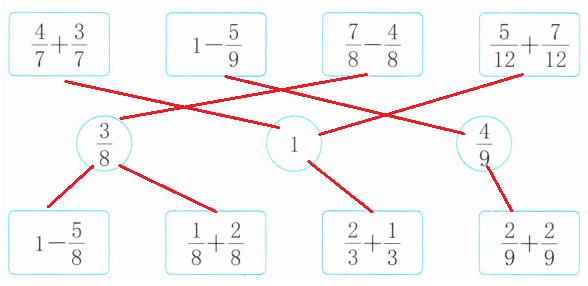
2. 连一连。

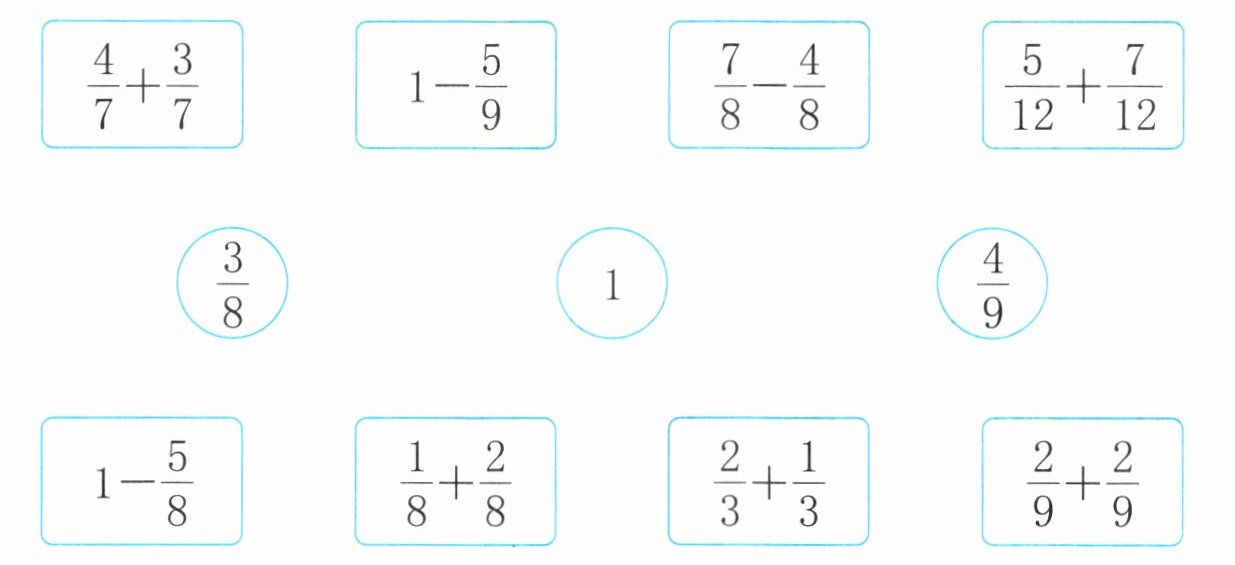
答案：

3. 学校举行爱心义卖,上午卖出了全部物品的$\frac{3}{7}$,下午卖出的物品和上午卖出的同样多。一天共卖出全部物品的几分之几?还剩几分之几?

答案： 解析：
本题考查分数的加法运算和减法运算。
上午卖出了全部物品的$\frac{3}{7}$，下午卖出的物品和上午卖出的同样多，也就是下午也卖出了全部物品的$\frac{3}{7}$。
那么一天共卖出的物品就是上午和下午卖出的物品之和，即：
$\frac{3}{7} + \frac{3}{7} = \frac{6}{7}$
还剩下的物品就是全部物品减去已经卖出的物品，即：
$1 - \frac{6}{7} = \frac{1}{7}$
答案：
一天共卖出全部物品的$\frac{6}{7}$，还剩$\frac{1}{7}$。

*4. 学校有一块长方形劳动基地,其中$\frac{1}{4}$种胡萝卜,剩下的$\frac{1}{3}$种小西红柿。画一画,比一比,胡萝卜与小西红柿这两块地,哪块更大?

答案：
解析：本题考查分数的初步认识中，对分数乘法意义的理解以及分数大小的比较。通过画图的方式，先求出种小西红柿的地占整个长方形劳动基地的几分之几，再与种胡萝卜的地占比进行比较。
答案：

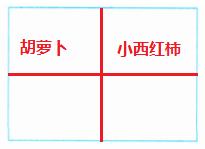
把整个长方形劳动基地看作单位“$1$”，种胡萝卜的地占$\frac{1}{4}$，剩下的地占$1 - \frac{1}{4} = \frac{3}{4}$。
因为剩下的$\frac{1}{3}$种小西红柿，所以种小西红柿的地占整个长方形劳动基地的$\frac{3}{4}×\frac{1}{3} = \frac{1}{4}$。
因为$\frac{1}{4}=\frac{1}{4}$，所以胡萝卜与小西红柿这两块地一样大。