《2025年作业本浙江教育出版社三年级数学上册人教版》

1. 在下面左边的长方体中,▲和★在相对的面上。请在右边长方体的展开图中标出★的位置。
→

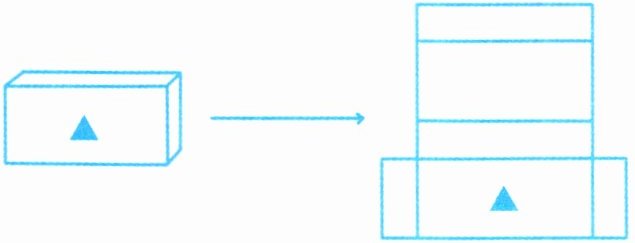
答案：

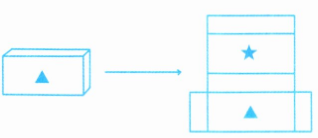
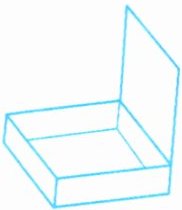
(1)如右图,把这个长方体纸盒剪开,平铺在桌面上,还需要剪开(B)条边。

A.1
B.4
C.7

答案： 本题可根据长方体的特征以及展开图的性质来确定还需要剪开的边的数量。
分析
长方体有$12$条棱，$6$个面。要把长方体纸盒剪开平铺在桌面上，使其成为一个展开图，需要剪开$7$条棱。
观察所给图形，已经有$3$条棱被剪开（图中显示断开的棱），那么还需要剪开的边的数量为：$7 - 3=4$（条）。
答案
B。

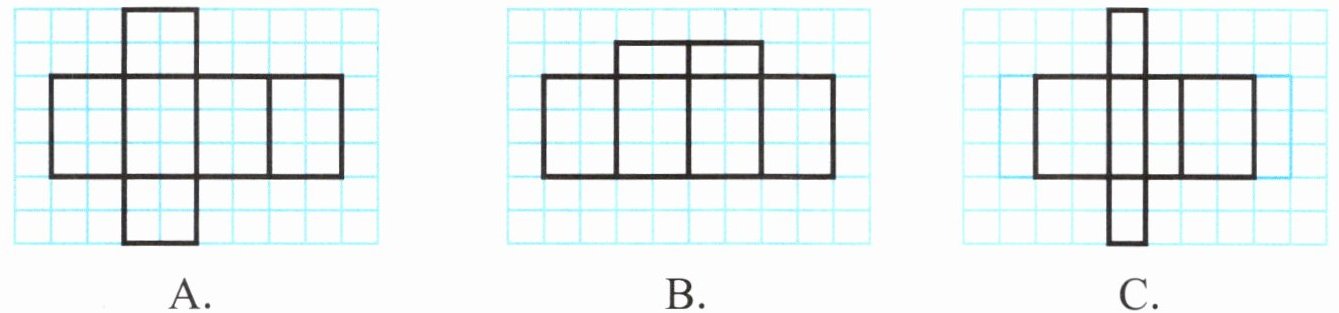
(2)下面各展开图可以围成长方体的是(A)。

答案： A

*3. “六连方”指的是由6个大小相同的正方形边与边相连拼成的图形(如图①)。你还能画出不同的“六连方”吗？画一画。你画的“六连方”中哪些能够折成正方体？在它的下面画“√”。

答案：