《2025年作业本浙江教育出版社三年级数学上册人教版》

1. 口算。
100×8=800 230×3=690 101×4=404 0＋95=95 2×43=86
100＋8=108 320×3=960 4×110=440 0×95=0 34×2=68

答案： 解析：这些题目都是基础的乘法与加法口算题，主要考查学生对于乘法和加法的掌握情况。
答案：
100×8=800
230×3=690
101×4=404
0＋95=95
2×43=86
100＋8=108
320×3=960
4×110=440
0×95=0
34×2=68

2. 列竖式计算。
809×7= 809
× 7
-----
5663 550×8= 550
× 8
-----
4400 243×9= 243
× 9
-----
2187 375×6= 375
× 6
-----
2250

答案：

3. 在○里填上“＞”“＜”或“＝”。
695×3＜2100 9×57＝57×9 5600＜826×7
215＋215＋215＋215＝215×4 195×8＞198×5

答案： 695×3＜2100
9×57＝57×9
5600＜826×7
215＋215＋215＋215＝215×4
195×8＞198×5

(1) 280×5,积的末尾有(B)个0。
A.1
B.2
C.3

答案： 解析：本题考查整数乘法运算以及对积末尾0的个数的判断。需要先计算出$280×5$的结果，再数积的末尾0的个数。
计算$280×5$时，可先计算$28×5 = 140$，然后在积的末尾添上1个0，即$280×5=1400$。
答案：B。

(2) 下列说法正确的是(C)。
A.如果因数中间没有0,那么积的中间一定没有0
B.如果因数中间有0,那么积的中间一定有0
C.如果因数末尾有0,那么积的末尾一定有0

答案： 解析：本题考查的知识点是乘法运算中积的特征。
A选项：如果因数中间没有0，积的中间可能有0，如$24× 5 = 120$，因数中间没有0，但积的中间有0，所以A选项错误。
B选项：如果因数中间有0，积的中间不一定有0，如$105× 3 = 315$，因数中间有0，但积的中间没有0，所以B选项错误。
C选项：如果因数末尾有0，那么积的末尾一定有0，因为0乘任何数都得0，所以C选项正确。
答案：C。

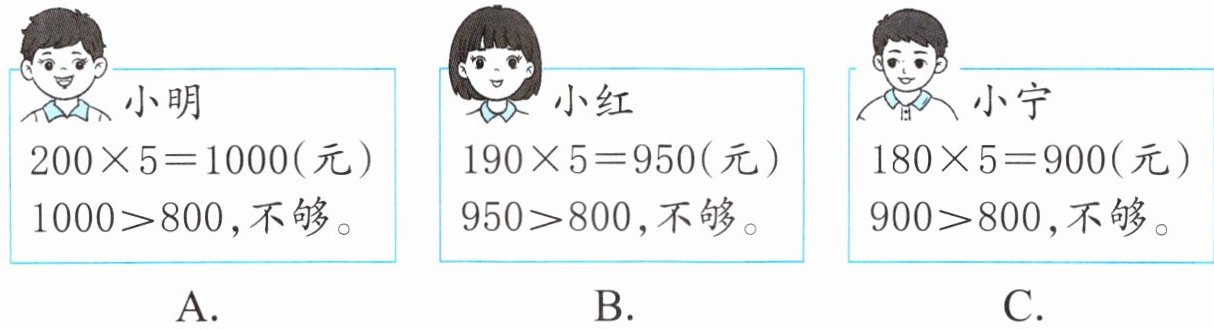
(3) 张叔叔买5张同样价格的高铁票,每张187元,800元钱够吗?下列解答合理的是(B)。
小明
200×5= 1000(元)
1000＞800,不够。
小红
190×5= 950(元)
950＞800,不够。
小宁
180×5= 900(元)
900＞800,不够。

答案： 解析：本题考查三位数乘一位数的估算。
在估算时，一般把三位数看成与它接近的整百数、几百几十数，再进行计算。
小明把$187$元看成$200$元，$200×5 = 1000$（元），因为$200$比$187$大，所以实际花费一定小于$1000$元，但无法准确判断与$800$元的大小关系，这种估算方法不太合理。
小红把$187$元看成$190$元，$190×5=950$（元），$190$接近$187$，且$950\gt800$，能合理判断出$800$元不够，这种估算方法合理。
小宁把$187$元看成$180$元，$180×5 = 900$（元），$180$比$187$小，实际花费大于$900$元，进而可以推出大于$800$元，这种估算方法合理，但相比小红的估算，与准确值偏差稍大。
综合来看，小红的估算更接近准确值且能合理判断，所以解答合理的是小红的方法。
答案：B。