《2025年作业本浙江教育出版社三年级数学上册人教版》

(1)学校运动场的环形跑道1圈是200米,(5)圈正好是1千米。

答案： 解析：本题主要考查长度单位的换算以及除法运算。需要先统一单位，再用总长度除以每圈的长度得到圈数。
因为$1千米 = 1000米$，已知环形跑道$1$圈是$200$米，要求多少圈正好是$1$千米，就是求$1000$米里面有多少个$200$米，用除法计算，即$1000÷200 = 5$（圈）。
答案：5

(2)某公园的人行步道长100米,如果走1千米,要走(10)个这样的长度。

答案： 解析：本题考查的是长度单位的换算以及简单的除法运算。首先，需要将1千米换算成米，因为人行步道的长度是以米为单位的。然后，用换算后的长度除以人行步道的长度，就可以得到需要走几个人行步道的长度。
根据$1千米 = 1000米$，
计算需要走几个人行步道的长度：$1000 ÷ 100 = 10(个)$。
答案：10。

(3)马拉松比赛全程约是42千米。一次比赛中,组委会每6千米设置一个补给站,起点和终点均设补给站。李叔叔到第5个补给站时,跑了24千米。

答案： 解析：题目考查了长度单位的应用以及简单的数学推理。
首先，马拉松比赛全程约是42千米，这是一个常识性问题，马拉松的标准距离就是42.195千米，但在这里简化为42千米。
其次，关于李叔叔到第5个补给站时跑了多少千米的问题，需要根据题目中给出的“组委会每6千米设置一个补给站，起点和终点均设补给站”这一条件进行推理。
李叔叔到第5个补给站，他实际上已经经过了4段距离，每段距离是6千米。
因此，他跑的总距离是 $4 × 6 = 24(千米)$，但由于起点也有一个补给站，
所以到第5个补给站时，他确实已经跑了24千米（不包含起点到第一个补给站的距离，因为起点即第一个补给站）。
答案：千米；24。

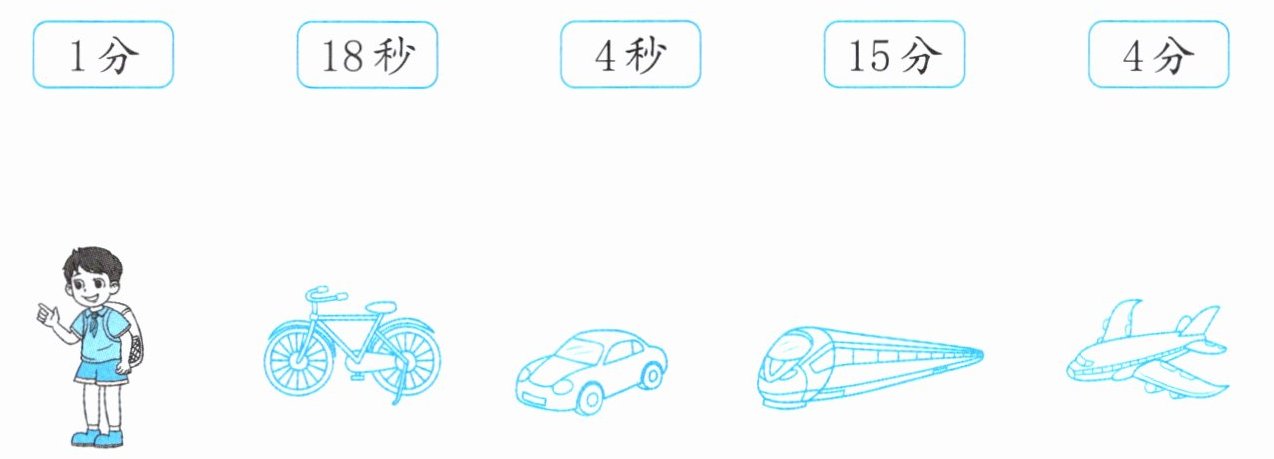
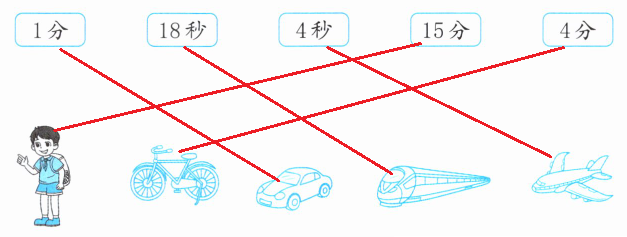
2. 用下面的出行方式行1千米,分别需要多长时间？连一连。

答案：

3. 将下面的长度按要求排列。
10千米 1000米 200厘米 10分米 999毫米
(999毫米)＜(10分米)＜(200厘米)＜(1000米)＜(10千米)

答案： 解析：本题考查不同长度单位之间的换算及比较大小。需要先将所有的长度单位统一换算成同一单位，比如都换算成米，然后再比较大小进行排列。
$10 千米=10×1000 米=10000 米$；
$200 厘米=200÷100 米=2 米$；
$10 分米=10÷10 米=1 米$；
$999 毫米=999÷1000 米=0.999 米$；
$999 毫米＜10 分米＜200 厘米＜1000 米＜10 千米$。
答案：999毫米 ＜ 10分米 ＜ 200厘米 ＜ 1000米 ＜ 10千米。

4. 古时候,人们用“一日千里”来形容马跑得很快。其中的“里”是我国古代用来计量路程的单位,2里等于1千米。

假设一只信鸽每小时飞行60千米,2小时最多能飞行多少里？

答案： 解析：本题可根据路程、速度、时间三者的关系先求出信鸽$2$小时飞行的千米数，再将千米数换算为里数。
步骤一：计算信鸽$2$小时飞行的千米数
根据路程$=$速度$×$时间，已知信鸽每小时飞行$60$千米，飞行时间为$2$小时，可得信鸽$2$小时飞行的千米数为：$60×2 = 120$（千米）
步骤二：将千米数换算为里数
已知$2$里等于$1$千米，那么$120$千米换算为里数为：$120×2 = 240$（里）
答案：$60×2×2 = 240$（里）
答：$2$小时最多能飞行$240$里。