《2025年作业本浙江教育出版社三年级数学上册人教版》

1. 填一填。
$\frac{5}{9}$里有(5)个$\frac{1}{9}$,再增加(4)个$\frac{1}{9}$就是1。

答案： 解析：
题目考查了分数的意义以及分数的加减法。
首先，我们需要确定$\frac{5}{9}$包含多少个$\frac{1}{9}$，这可以通过简单的除法来得出，即$\frac{5}{9} ÷ \frac{1}{9} = 5$。
接着，我们需要找出再增加多少个$\frac{1}{9}$，$\frac{5}{9}$就能变成1。
由于1可以表示为$\frac{9}{9}$，所以我们需要增加的分数就是$\frac{9}{9} - \frac{5}{9} = \frac{4}{9}$，
即再增加4个$\frac{1}{9}$。
答案：
5；4。

2. 如下图,有一满杯水,小红先喝了这杯水的$\frac{1}{2}$,又喝了这杯水的$\frac{1}{4}$,最后倒入这杯水的$\frac{3}{4}$。

答案： 解析：本题可根据图中杯子水位的变化情况，结合分数的意义来确定每次喝掉和倒入的水占这杯水的几分之几。
确定第一次喝掉的水占这杯水的几分之几：
观察第一幅图可知，杯子是满的，看作单位“$1$”；第二幅图中水位下降到原来的一半，说明喝掉了这杯水的一半，根据分数的意义，一半用分数表示为$\frac{1}{2}$，即小红先喝了这杯水的$\frac{1}{2}$。
确定第二次喝掉的水占这杯水的几分之几：
第二幅图中杯子还剩$\frac{1}{2}$杯水，第三幅图中水位又下降了一些，此时剩下的水是原来满杯水的$\frac{1}{4}$，那么第二次喝掉的水占这杯水的$\frac{1}{2}-\frac{1}{4}$。
对$\frac{1}{2}-\frac{1}{4}$进行通分计算，$\frac{1}{2}=\frac{2}{4}$，则$\frac{1}{2}-\frac{1}{4}=\frac{2}{4}-\frac{1}{4}=\frac{1}{4}$，即第二次喝了这杯水的$\frac{1}{4}$。
确定最后倒入的水占这杯水的几分之几：
第三幅图中杯子还剩$\frac{1}{4}$杯水，第四幅图中杯子是满的，说明倒入的水使杯子从$\frac{1}{4}$杯水变为满杯水，那么倒入的水占这杯水的$1 - \frac{1}{4}=\frac{3}{4}$。
答案：$\frac{1}{2}$；$\frac{1}{4}$；$\frac{3}{4}$。

(1) 妈妈做了一个蛋糕,平均分成5份,小明吃了$\frac{1}{5}$,爸爸吃的和小明吃的同样多。他俩一共吃了这个蛋糕的( ),还剩这个蛋糕的( )。
A.$\frac{2}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$

答案：
(1)A，B

(2) 一块巧克力,小亮吃了整块的$\frac{5}{8}$,弟弟比他吃得少一些。弟弟可能吃了这块巧克力的( )。

A.$\frac{6}{8}$
B.$\frac{4}{8}$
C.$\frac{3}{8}$

答案：
(2)C

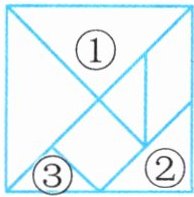
*4. 七巧板(如下图)是我国传统的游戏,它有3种大小不同的三角形。这三种三角形分别占整个正方形的几分之几?比一比这三个分数的大小。

答案： 解析：本题考查分数的意义以及分数大小比较的知识点。
将正方形平均分成16个与图③相同的三角形，图①占4份，图②占2份，图③占1份。
图①占整个正方形的$\frac{4}{16}$，即$\frac{1}{4}$；
图②占整个正方形的$\frac{2}{16}$，即$\frac{1}{8}$；
图③占整个正方形的$\frac{1}{16}$。
分母越大，分数越小，所以$\frac{1}{4}＞\frac{1}{8}＞\frac{1}{16}$。
答案：图①占整个正方形的$\frac{1}{4}$，图②占整个正方形的$\frac{1}{8}$，图③占整个正方形的$\frac{1}{16}$；$\frac{1}{4}＞\frac{1}{8}＞\frac{1}{16}$。