《2025年课时练人民教育出版社八年级数学上册人教版》

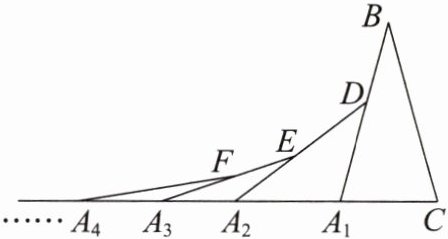
8. 如图,在第$1个\triangle A_1BC$中,$\angle B = 30^{\circ}$,$A_1B = CB$；在边$A_1B上任取一点D$,延长$CA_1到A_2$,使$A_1A_2 = A_1D$,得到第$2个\triangle A_1A_2D$；在边$A_2D上任取一点E$,延长$A_1A_2到A_3$,使$A_2A_3 = A_2E$,得到第$3个\triangle A_2A_3E$,……$$按此做法继续下去,则第$n个三角形中以A_n$为顶点的内角的度数是(C)

A.$(\frac{1}{2})^n \cdot 75^{\circ}$
B.$(\frac{1}{2})^{n - 1} \cdot 65^{\circ}$
C.$(\frac{1}{2})^{n - 1} \cdot 75^{\circ}$
D.$(\frac{1}{2})^n \cdot 85^{\circ}$

答案： C

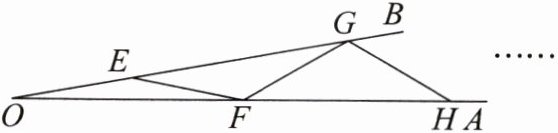
9. 如图所示,$\angle AOB$是一个钢架的示意图,且$\angle AOB = 10^{\circ}$,为了使钢架更加坚固,需在其内部添加一些钢管$EF$,$FG$,$GH$,…$$,添加的钢管的长度都与$OE$相等,则最多能添加8根这样的钢管。

答案： 8

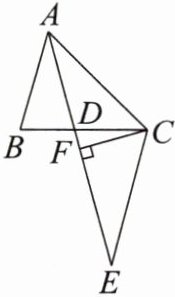
10. 如图,在$\triangle ABC$中,$AD是\angle BAC$的平分线,点$D在BC$上,且$AD = AB$,过点$C作AB$的平行线,交$AD的延长线于点E$,$CF \perp AE于点F$。请你用等式表示线段$AF$,$AB$,$AC$之间的数量关系,并证明。

答案： 解:2AF=AB+AC.证明如下:
因为AD是∠BAC的平分线,
所以∠BAD=∠CAD.
因为AB//CE,
所以∠B=∠BCE,∠BAD=∠E,
所以∠CAD=∠E,所以AC=CE.
因为AB=AD,所以∠B=∠ADB,
所以∠BCE=∠ADB.
因为∠ADB=∠CDE,
所以∠BCE=∠CDE,
所以CE=ED,所以AC=CE=ED.
因为CF⊥AE,所以AE=2AF.
因为AE=AD+ED,
所以AE=AB+AC,
所以2AF=AB+AC.

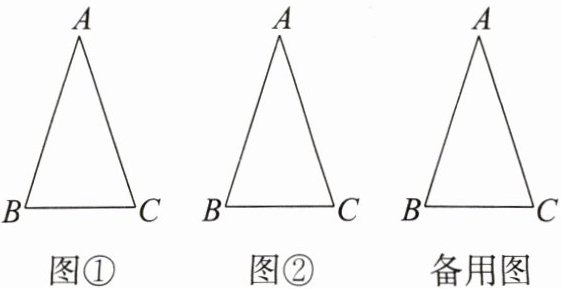
11. (新定义题)如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,称满足此条件的三角形为黄金等腰三角形。请完成以下操作：(以下问题所指的等腰三角形个数均不包括$\triangle ABC$)
(1)在图①中画$1$条线段,使图①中有$2$个等腰三角形,并直接写出这$2$个等腰三角形的顶角的度数；
(2)在图②中画$2$条线段,使图②中有$4$个等腰三角形；
(3)继续按以上操作发现：在$\triangle ABC中画n$条线段,则图中有______个等腰三角形,其中有______个黄金等腰三角形。

答案：
解:
(1)如图①所示,因为AB=AC,∠A=36°,
所以当AE=BE时,∠A=∠ABE=36°,则∠AEB=108°,所以∠EBC=36°,
所以这2个等腰三角形的顶角的度数分别是108°和36°(画法不唯一).
(2)如图②所示(画法不唯一).
(3)由上述可知,画1条线段可得到2个等腰三角形,其中有1个黄金等腰三角形;
画2条线段可得到4个等腰三角形,其中有2个黄金等腰三角形;
如图③所示,画3条线段可得到6个等腰三角形,其中有3个黄金等腰三角形;
……
所以在△ABC中画n条线段,则图中有2n个等腰三角形,其中有n个黄金等腰三角形.故答案为2n;n.