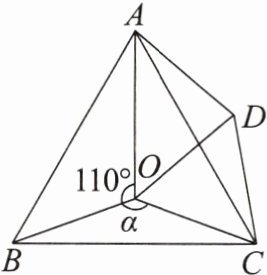
8. 如图,点 $ O $ 是等边三角形 $ ABC $ 内一点,点 $ D $ 是 $ \triangle ABC $ 外的一点,$ \angle AOB = 110^{\circ} $,$ \angle BOC = \alpha $,$ \triangle BOC \cong \triangle ADC $,$ \angle OCD = 60^{\circ} $,连接 $ OD $。
(1) 求证:$ \triangle OCD $ 是等边三角形;
(2) 当 $ \alpha = 150^{\circ} $ 时,试判断 $ \triangle AOD $ 的形状,并说明理由;
(3) 探究:当 $ \alpha $ 为多少度时,$ \triangle AOD $ 是等腰三角形。
(1) 求证:$ \triangle OCD $ 是等边三角形;
(2) 当 $ \alpha = 150^{\circ} $ 时,试判断 $ \triangle AOD $ 的形状,并说明理由;
(3) 探究:当 $ \alpha $ 为多少度时,$ \triangle AOD $ 是等腰三角形。

答案:
(1)证明:因为$\triangle BOC\cong \triangle ADC$,
所以$OC=DC$.
因为$\angle OCD=60^{\circ }$,
所以$\triangle OCD$是等边三角形.
(2)解:$\triangle AOD$是直角三角形.理由如下:
因为$\triangle OCD$是等边三角形,
所以$\angle ODC=60^{\circ }$.
因为$\triangle BOC\cong \triangle ADC$,$\alpha =150^{\circ }$,
所以$\angle ADC=\angle BOC=\alpha =150^{\circ }$,
所以$\angle ADO=\angle ADC - \angle ODC=150^{\circ } - 60^{\circ }=90^{\circ }$,所以$\triangle AOD$是直角三角形.
(3)解:因为$\triangle OCD$是等边三角形,
所以$\angle COD=\angle ODC=60^{\circ }$.
因为$\angle AOB=110^{\circ }$,$\angle ADC=\angle BOC=\alpha $,
所以$\angle AOD=360^{\circ } - \angle AOB - \angle BOC - \angle COD=360^{\circ } - 110^{\circ } - \alpha - 60^{\circ }=190^{\circ } - \alpha $,
$\angle ADO=\angle ADC - \angle ODC=\alpha - 60^{\circ }$,
所以$\angle OAD=180^{\circ } - \angle AOD - \angle ADO=180^{\circ } - (190^{\circ } - \alpha ) - (\alpha - 60^{\circ })=50^{\circ }$.
①当$\angle AOD=\angle ADO$时,即$190^{\circ } - \alpha =\alpha - 60^{\circ }$,
所以$\alpha =125^{\circ }$.
②当$\angle AOD=\angle OAD$时,即$190^{\circ } - \alpha =50^{\circ }$,
所以$\alpha =140^{\circ }$.
③当$\angle ADO=\angle OAD$时,即$\alpha - 60^{\circ }=50^{\circ }$,
所以$\alpha =110^{\circ }$.
综上所述,当$\alpha =110^{\circ }$或$125^{\circ }$或$140^{\circ }$时,
$\triangle AOD$是等腰三角形.
(1)证明:因为$\triangle BOC\cong \triangle ADC$,
所以$OC=DC$.
因为$\angle OCD=60^{\circ }$,
所以$\triangle OCD$是等边三角形.
(2)解:$\triangle AOD$是直角三角形.理由如下:
因为$\triangle OCD$是等边三角形,
所以$\angle ODC=60^{\circ }$.
因为$\triangle BOC\cong \triangle ADC$,$\alpha =150^{\circ }$,
所以$\angle ADC=\angle BOC=\alpha =150^{\circ }$,
所以$\angle ADO=\angle ADC - \angle ODC=150^{\circ } - 60^{\circ }=90^{\circ }$,所以$\triangle AOD$是直角三角形.
(3)解:因为$\triangle OCD$是等边三角形,
所以$\angle COD=\angle ODC=60^{\circ }$.
因为$\angle AOB=110^{\circ }$,$\angle ADC=\angle BOC=\alpha $,
所以$\angle AOD=360^{\circ } - \angle AOB - \angle BOC - \angle COD=360^{\circ } - 110^{\circ } - \alpha - 60^{\circ }=190^{\circ } - \alpha $,
$\angle ADO=\angle ADC - \angle ODC=\alpha - 60^{\circ }$,
所以$\angle OAD=180^{\circ } - \angle AOD - \angle ADO=180^{\circ } - (190^{\circ } - \alpha ) - (\alpha - 60^{\circ })=50^{\circ }$.
①当$\angle AOD=\angle ADO$时,即$190^{\circ } - \alpha =\alpha - 60^{\circ }$,
所以$\alpha =125^{\circ }$.
②当$\angle AOD=\angle OAD$时,即$190^{\circ } - \alpha =50^{\circ }$,
所以$\alpha =140^{\circ }$.
③当$\angle ADO=\angle OAD$时,即$\alpha - 60^{\circ }=50^{\circ }$,
所以$\alpha =110^{\circ }$.
综上所述,当$\alpha =110^{\circ }$或$125^{\circ }$或$140^{\circ }$时,
$\triangle AOD$是等腰三角形.
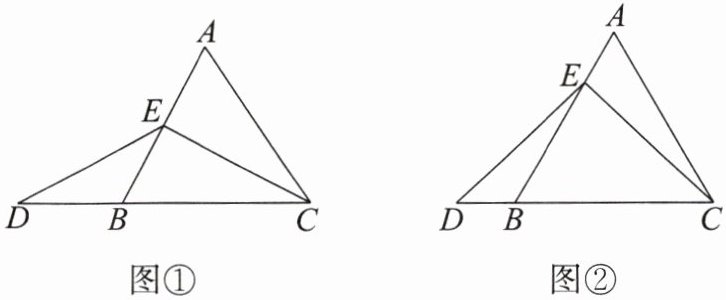
9. 已知在等边三角形 $ ABC $ 中,点 $ E $ 在 $ AB $ 上,点 $ D $ 在 $ CB $ 的延长线上,且 $ ED = EC $。
(1) 【特殊情况,探索结论】
如图①,当点 $ E $ 为 $ AB $ 的中点时,确定线段 $ AE $ 与 $ DB $ 的大小关系,请你直接写出结论:$ AE $______$ DB $(填“$ > $”“$ < $”或“$ = $”)。
(2) 【特例启发,解答题目】
如图②,当点 $ E $ 为 $ AB $ 边上任意一点时,确定线段 $ AE $ 与 $ DB $ 的大小关系,并说明理由。
(3) 【拓展结论,设计新题】
在等边三角形 $ ABC $ 中,点 $ E $ 在直线 $ AB $ 上,点 $ D $ 在线段 $ CB $ 的延长线上,且 $ ED = EC $,若 $ \triangle ABC $ 的边长为 $ 1 $,$ AE = 2 $,求 $ CD $ 的长(请你画出相应图形,并直接写出结果)。
(1) 【特殊情况,探索结论】
如图①,当点 $ E $ 为 $ AB $ 的中点时,确定线段 $ AE $ 与 $ DB $ 的大小关系,请你直接写出结论:$ AE $______$ DB $(填“$ > $”“$ < $”或“$ = $”)。
(2) 【特例启发,解答题目】
如图②,当点 $ E $ 为 $ AB $ 边上任意一点时,确定线段 $ AE $ 与 $ DB $ 的大小关系,并说明理由。
(3) 【拓展结论,设计新题】
在等边三角形 $ ABC $ 中,点 $ E $ 在直线 $ AB $ 上,点 $ D $ 在线段 $ CB $ 的延长线上,且 $ ED = EC $,若 $ \triangle ABC $ 的边长为 $ 1 $,$ AE = 2 $,求 $ CD $ 的长(请你画出相应图形,并直接写出结果)。

答案:
(1)=
(2)$AE=DB$.理由如下:
如图,过点E作$EF// BC$,交AC于点F.

因为$\triangle ABC$为等边三角形,
所以$\triangle AEF$为等边三角形,
所以$AE=EF=AF$,所以$BE=CF$.
因为$ED=EC$,所以$\angle D=\angle ECD$.
因为$\angle DEB=60^{\circ } - \angle D$,$\angle ECF=60^{\circ } - \angle ECD$,
所以$\angle DEB=\angle ECF$.
在$\triangle DBE$和$\triangle EFC$中,
$\left\{\begin{array}{l} DE=EC,\\ \angle DEB=\angle ECF,\\ BE=FC,\end{array}\right. $
所以$\triangle DBE\cong \triangle EFC(SAS)$,
所以$DB=EF$,所以$AE=DB$.
(3)当点E在AB的延长线上时,作$EF// AC$,交CB的延长线于点F,则$\triangle EFB$为等边三角形,如图所示,可得$\triangle DBE\cong \triangle CFE$.

因为$AB=1$,$AE=2$,所以$BE=1$,
所以$BF=BE=1$.
因为$DB=FC=BF + BC=2$,
所以$CD=BC + DB=3$.
当点E在BA的延长线上时,不存在点D在CB延长线上,使$ED=EC$.
综上所述,$CD=3$.
(1)=
(2)$AE=DB$.理由如下:
如图,过点E作$EF// BC$,交AC于点F.

因为$\triangle ABC$为等边三角形,
所以$\triangle AEF$为等边三角形,
所以$AE=EF=AF$,所以$BE=CF$.
因为$ED=EC$,所以$\angle D=\angle ECD$.
因为$\angle DEB=60^{\circ } - \angle D$,$\angle ECF=60^{\circ } - \angle ECD$,
所以$\angle DEB=\angle ECF$.
在$\triangle DBE$和$\triangle EFC$中,
$\left\{\begin{array}{l} DE=EC,\\ \angle DEB=\angle ECF,\\ BE=FC,\end{array}\right. $
所以$\triangle DBE\cong \triangle EFC(SAS)$,
所以$DB=EF$,所以$AE=DB$.
(3)当点E在AB的延长线上时,作$EF// AC$,交CB的延长线于点F,则$\triangle EFB$为等边三角形,如图所示,可得$\triangle DBE\cong \triangle CFE$.

因为$AB=1$,$AE=2$,所以$BE=1$,
所以$BF=BE=1$.
因为$DB=FC=BF + BC=2$,
所以$CD=BC + DB=3$.
当点E在BA的延长线上时,不存在点D在CB延长线上,使$ED=EC$.
综上所述,$CD=3$.
查看更多完整答案,请扫码查看


