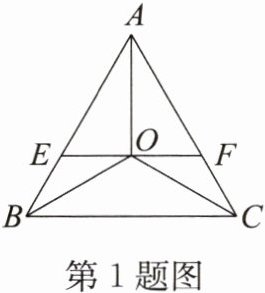
1. 如图,等边三角形 $ ABC $ 的三条角平分线相交于点 $ O $,过点 $ O $ 作 $ EF // BC $ 交 $ AB $ 于点 $ E $,交 $ AC $ 于点 $ F $,那么这个图形中的等腰三角形共有(
A.4 个
B.5 个
C.6 个
D.7 个
D
)
A.4 个
B.5 个
C.6 个
D.7 个
答案:
D
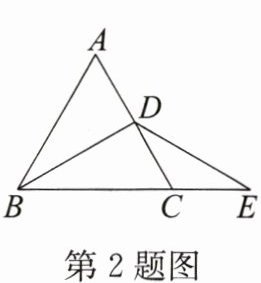
2. 如图,$ \triangle ABC $ 是等边三角形,$ AB = 6 $,$ BD $ 是 $ \angle ABC $ 的平分线,延长 $ BC $ 到点 $ E $,使 $ CE = CD $,则 $ BE $ 的长为(
A.7
B.8
C.$ \frac{17}{2} $
D.9
D
)
A.7
B.8
C.$ \frac{17}{2} $
D.9
答案:
D
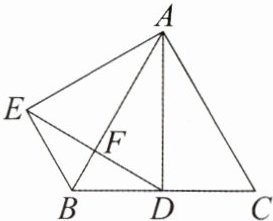
3. 如图,$ \triangle ABC $ 是等边三角形,$ AD $ 是 $ \triangle ABC $ 的角平分线,$ \triangle ADE $ 是等边三角形,$ AB $ 与 $ ED $ 相交于点 $ F $,有下列结论:① $ AD \perp BC $;② $ EF = FD $;③ $ BE = BD $。其中正确的个数为(
A.0
B.1
C.2
D.3
D
)
A.0
B.1
C.2
D.3
答案:
D
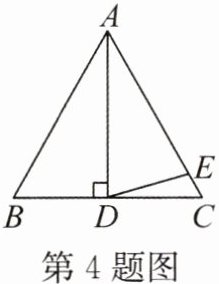
4. 如图,$ \triangle ABC $ 是等边三角形,$ AD \perp BC $ 于点 $ D $,$ AE = AD $,则 $ \angle CDE = $
$15^{\circ }$
。
答案:
$15^{\circ }$
5. 如图,$ OP $ 平分 $ \angle AOB $,$ \angle AOP = 15^{\circ} $,$ PC // OA $,$ PD \perp OA $ 于点 $ D $,$ PC = 4 $,则 $ PD = $
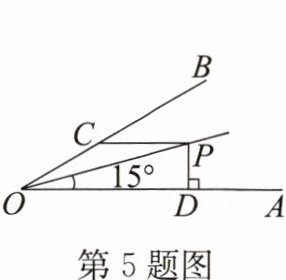
2
。
答案:
2
6. 如图,已知 $ \angle O = 60^{\circ} $,点 $ C $ 在 $ OB $ 上,$ OC = 8 $,点 $ D $,$ E $ 在 $ OA $ 上,且 $ CD = CE $。若 $ DE = 4 $,则 $ OE $ 的长为
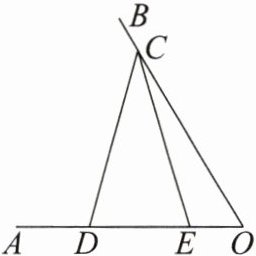
2
。
答案:
2
7. 如图,已知 $ \triangle ABC $ 为等边三角形,$ D $ 为 $ BC $ 延长线上的一点,$ CE $ 平分 $ \angle ACD $,$ CE = BD $,求证:$ \triangle ADE $ 是等边三角形。
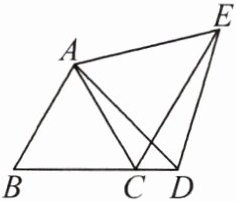

答案:
证明:因为$\triangle ABC$为等边三角形,
所以$AB=AC$,$\angle B=\angle ACB=60^{\circ }$,
所以$\angle ACD=120^{\circ }$.
又因为CE平分$\angle ACD$,
所以$\angle ACE=60^{\circ }$,所以$\angle B=\angle ACE$.
又因为$BD=CE$,
所以$\triangle ABD\cong \triangle ACE(SAS)$,
所以$\angle BAD=\angle CAE$,$AD=AE$,
所以$\angle CAE - \angle CAD=\angle BAD - \angle CAD$,
即$\angle EAD=\angle BAC=60^{\circ }$.
又因为$AD=AE$,
所以$\triangle ADE$是等边三角形.
所以$AB=AC$,$\angle B=\angle ACB=60^{\circ }$,
所以$\angle ACD=120^{\circ }$.
又因为CE平分$\angle ACD$,
所以$\angle ACE=60^{\circ }$,所以$\angle B=\angle ACE$.
又因为$BD=CE$,
所以$\triangle ABD\cong \triangle ACE(SAS)$,
所以$\angle BAD=\angle CAE$,$AD=AE$,
所以$\angle CAE - \angle CAD=\angle BAD - \angle CAD$,
即$\angle EAD=\angle BAC=60^{\circ }$.
又因为$AD=AE$,
所以$\triangle ADE$是等边三角形.
查看更多完整答案,请扫码查看


