1. 如图,$AB = AC$,$BD\perp AC于点D$,$CE\perp AB于点E$,图中全等三角形的组数是(
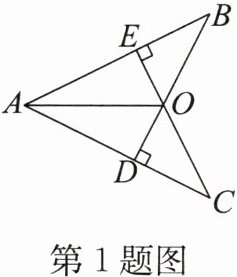
A.2
B.3
C.4
D.5
C
)
A.2
B.3
C.4
D.5
答案:
C
2. 如图所示,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$D为AB$上一点,且$BD = BC$,$ED\perp AB$,点$D$为垂足,如果$AC = 8\mathrm{cm}$,那么$AE + DE = $
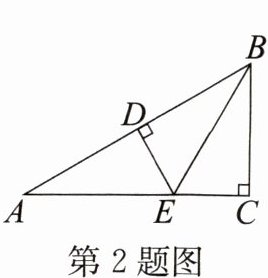
8
$\mathrm{cm}$。
答案:
8
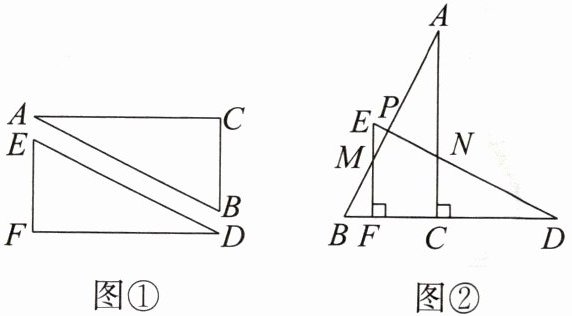
3. 一张长方形纸片沿对角线剪开,得到两张三角形纸片如图①所示,再将两张三角形纸片摆成如图②所示的形式,使点$B$,$F$,$C$,$D$在同一条直线上。
(1)求证:$AB\perp DE$。
(2)若$PB = BC$,请找出图中与此条件有关的一对全等三角形,并给予说明。
(1)求证:$AB\perp DE$。
(2)若$PB = BC$,请找出图中与此条件有关的一对全等三角形,并给予说明。

答案:
3.
(1)证明:由已知条件,易得△ABC≌△DEF,则有∠A=∠D.又∠ANP=∠DNC,所以∠APN=∠DCN=90°,即AB⊥DE.
(2)解:△PBD≌△CBA.理由如下:
由
(1)可得∠BPD=90°,
所以∠BPD=∠BCA.
在△PBD和△CBA中,
∠BPD=∠BCA,
PB=BC,
∠PBD=∠CBA,
所以△PBD≌△CBA(ASA).
(1)证明:由已知条件,易得△ABC≌△DEF,则有∠A=∠D.又∠ANP=∠DNC,所以∠APN=∠DCN=90°,即AB⊥DE.
(2)解:△PBD≌△CBA.理由如下:
由
(1)可得∠BPD=90°,
所以∠BPD=∠BCA.
在△PBD和△CBA中,
∠BPD=∠BCA,
PB=BC,
∠PBD=∠CBA,
所以△PBD≌△CBA(ASA).
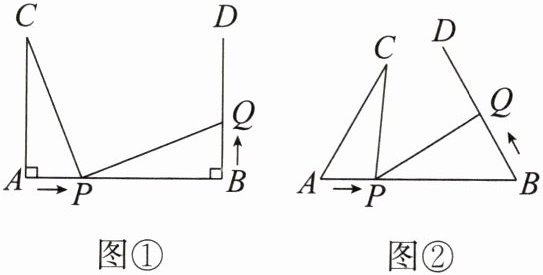
4. 如图①,$AB = 7\mathrm{cm}$,$AC\perp AB$,$BD\perp AB$,垂足分别为$A$,$B$,$AC = 5\mathrm{cm}$。点$P在线段AB上以2\mathrm{cm/s}的速度由点A向点B$运动,同时点$Q在射线BD$上运动,它们运动的时间为$t\mathrm{s}$(当点$P$运动结束时,点$Q$运动随之结束)。
(1)若点$Q的运动速度与点P$的运动速度相等,当$t = 1$时,判断$\triangle ACP与\triangle BPQ$是否全等,并判断此时线段$PC和线段PQ$的位置关系,请分别说明理由。
(2)如图②,若将“$AC\perp AB$,$BD\perp AB$”改为“$\angle CAB = \angle DBA$”,点$Q的运动速度为x\mathrm{cm/s}$,其他条件不变,当$x$的值为多少时,$\triangle ACP与\triangle BPQ$全等?
(1)若点$Q的运动速度与点P$的运动速度相等,当$t = 1$时,判断$\triangle ACP与\triangle BPQ$是否全等,并判断此时线段$PC和线段PQ$的位置关系,请分别说明理由。
(2)如图②,若将“$AC\perp AB$,$BD\perp AB$”改为“$\angle CAB = \angle DBA$”,点$Q的运动速度为x\mathrm{cm/s}$,其他条件不变,当$x$的值为多少时,$\triangle ACP与\triangle BPQ$全等?

答案:
4.解:
(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:因为AC⊥AB,BD⊥AB,
所以∠A=∠B=90°.
当t=1时,AP=BQ=2 cm,
所以BP=AB-AP=7-2=5(cm),
所以BP=AC.
在△ACP和△BPQ中,
AP=BQ,
∠A=∠B,
AC=BP,
所以△ACP≌△BPQ(SAS).
所以∠C=∠BPQ.
因为∠C+∠APC=90°,
所以∠APC+∠BPQ=90°,
所以∠CPQ=90°,所以PC⊥PQ.
(2)x的值为2或$\frac{20}{7}$时,△ACP与△BPQ全等.
(1)△ACP≌△BPQ,PC⊥PQ.
理由如下:因为AC⊥AB,BD⊥AB,
所以∠A=∠B=90°.
当t=1时,AP=BQ=2 cm,
所以BP=AB-AP=7-2=5(cm),
所以BP=AC.
在△ACP和△BPQ中,
AP=BQ,
∠A=∠B,
AC=BP,
所以△ACP≌△BPQ(SAS).
所以∠C=∠BPQ.
因为∠C+∠APC=90°,
所以∠APC+∠BPQ=90°,
所以∠CPQ=90°,所以PC⊥PQ.
(2)x的值为2或$\frac{20}{7}$时,△ACP与△BPQ全等.
查看更多完整答案,请扫码查看


