《2025年课时练人民教育出版社八年级数学上册人教版》

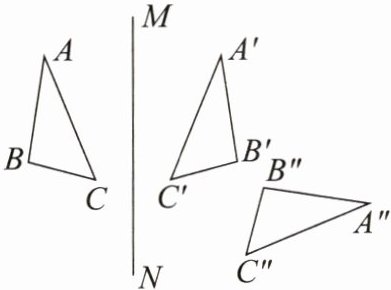
8. 如图,$\triangle ABC与\triangle A'B'C'关于直线MN$对称,$\triangle A'B'C'与\triangle A''B''C''关于直线EF$对称.
(1)画出直线$EF$；
(2)若直线$MN与EF相交于点O$,试探究$\angle BOB''与直线MN$,$EF所夹锐角\alpha$的数量关系.

答案：
解:
(1)如图,连接B'B'',作线段B'B''的垂直平分线EF,则直线EF即为所求.

(2)如图,连接BO,B'O,B''O.
因为△ABC与△A'B'C'关于直线MN对称,所以∠BOM=∠B'OM.
又因为△A'B'C'与△A''B''C''关于直线EF对称,所以∠B'OE=∠B''OE.
所以∠BOB''=∠BOM+∠B'OM+∠B'OE+∠B''OE=2(∠B'OM+∠B'OE)=2∠MOE=2α.

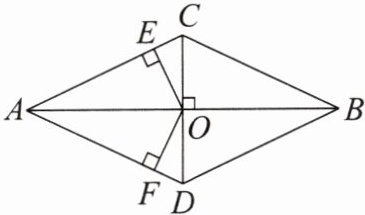
9. 如图,在四边形$ADBC$中,$AB与CD$互相垂直平分,垂足为$O$. 若$OE$,$OF分别是点O到\angle CAD$两边的距离,试说明它们之间的大小关系.

答案： OE=OF.

10. 【问题发现】我们知道“线段垂直平分线上的点与这条线段两个端点的距离相等”,那么不在线段垂直平分线上的点与这条线段两个端点的距离大小如何判断呢？
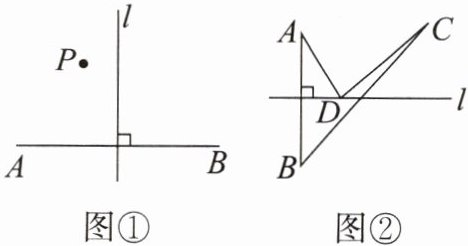
【自主探究】(1)如图①,直线$l是线段AB$的垂直平分线,点$P在直线l$的左侧,经测量,$PA\lt PB$,请证明这个结论.
【迁移应用】(2)如图②,直线$l是线段AB$的垂直平分线,点$C在直线l$外,且与点$A在直线l$的同侧,点$D是直线l$上的任意一点,连接$AD$,$BC$,$CD$,试判断$BC和AD + CD$之间的大小关系,并说明理由.

答案：

(1)证明:如图①,连接PA,PB,PB与直线l交于点M,连接AM.
因为直线l是线段AB的垂直平分线,所以AM=BM,
所以PB=PM+BM=PM+AM.
因为PM+AM＞PA,所以PA＜PB.
　　　
(2)解:AD+CD≥BC.理由如下:
如图②,当D不在线段BC上时,连接BD.
因为直线l是线段AB的垂直平分线,所以AD=BD,
所以AD+CD=BD+CD＞BC.
当D在线段BC上时,AD+CD=BC,所以AD+CD≥BC.